NAMING COLLINEAR AND COPLANAR POINTS WORKSHEET

Question 1 :

Look at the figure given below and answer the questions. 

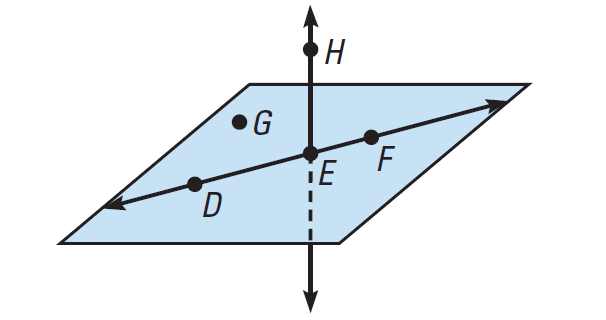
(i) Name three points that are collinear.

(ii) name four points that are coplanar.

(iii) Name three points that are not collinear.

Question 2 :

Draw three non collinear points, J, K and L. Then draw the lines JK, KL and LJ.

Question 3 :

Draw two lines, label points on the lines and name two pairs of opposite rays.

Question 4 :

Three points may be considered as the vertices of a triangle. But, the area of the triangle is zero. Then, what can we conclude about the three points?

Question 5 :

Three points may be considered as collinear. But, the area of the triangle formed by those three points is 23 square units. Then, what can we conclude about the three points?

Answers

1. Answer :

Part (i) :

Points D, E and F lie on the same line. So they are collinear.

Part (ii) :

Points D, E, F and G lie on the same plane. So they are coplanar. D, E, F and H are coplanar, even though the plane containing them is not drawn.

Part (iii) :

There are many correct answers. For instance, points H, E and G do not lie on the same line.

2. Answer :

Step 1 :

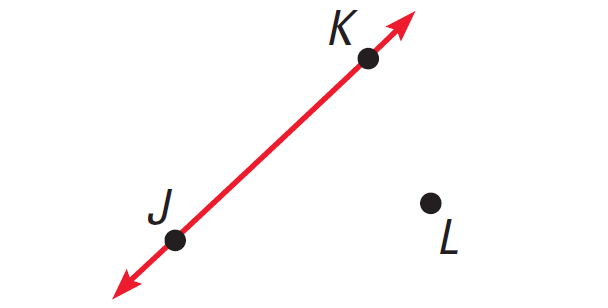
Draw the points J, K and L as given below.

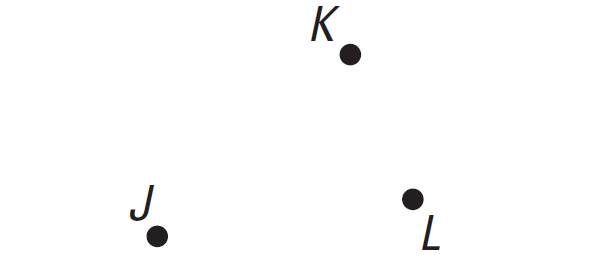
Step 2 :

Draw the line JK by connecting the points J and K as given below.

Step 3 :

Draw the line KL by connecting the points K and L as given below.

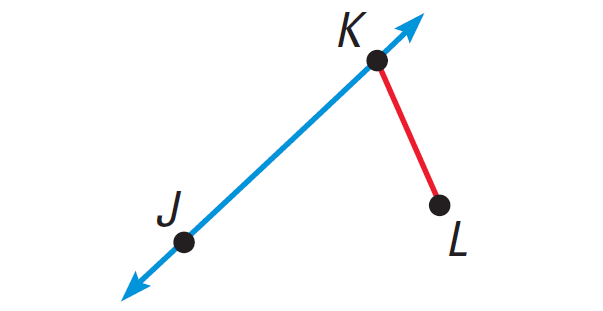
Step 4 :

Draw the line LJ by connecting the points L and J as given below.

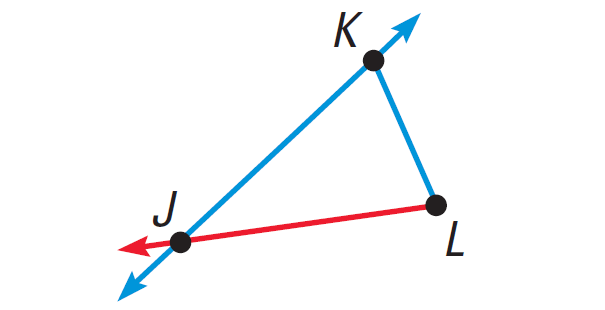
3. Answer :

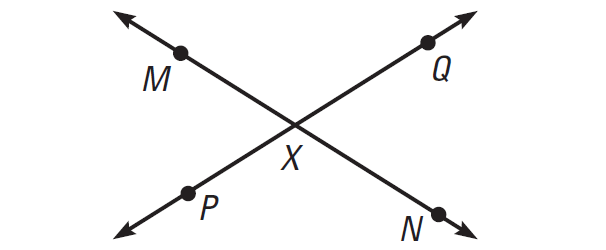
Points M, N and X are collinear and X is between M and N.

So, XM and XN are opposite rays.

Points P, Q and X are collinear and X is between P and Q.

So, XP and XQ are opposite rays.

4. Answer :

If the area of a triangle is zero, then the three points which are being as vertices must lie on the same line. So, the three points are collinear.

5. Answer :

Since the area of the triangle (23 square units) is not zero, the given three points form a triangle. Because, three points form a triangle, they do not lie on the same line.

Hence, the three points are not collinear.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.