MULTIPLYING RATIONAL NUMBERS WITH DIFFERENT SIGNS

If we want to multiply two rational numbers, first we have to multiply the signs of the numbers. 

The rules for the signs of products of rational numbers with different signs are summarized below.

Let p and q be rational numbers.

From the above rules, it is clear that when we multiply two rational numbers with different signs, the result is always negative. 

Example 1 : 

Multiply 2 and -1/4. 

Solution : 

Step 1 : 

In the two rational numbers 2 and -1/4, the signs are different. 

Step 2 : 

Find the product of 2 and 1/4

2 x 1/4  =  2/4  =  1/2 

Step 3 : 

Since we multiply two rational numbers with different signs, the result is always negative. 

So,

2 x (-1/4)  =  - 1/2.

Example 2 :

David has made three withdrawals of $2 each from his savings account. What was the change in his balance ?

Solution : 

To know the change in balance, we have to find 3(-2).

Making withdrawal from account will reduce the balance. To indicate the reduce in balance, we use negative sign. 

Since the withdrawal is made of $2, we can use "-2".  

To graph -2, we have to start at 0 and move 2 units to the left.

3(-2) means (-2) + (-2) + (-2)

To graph 3(-2), start at 0 and move 2 units to the left 3 times. 

(Here, we move to the left, because of the negative sign we have with "2" )

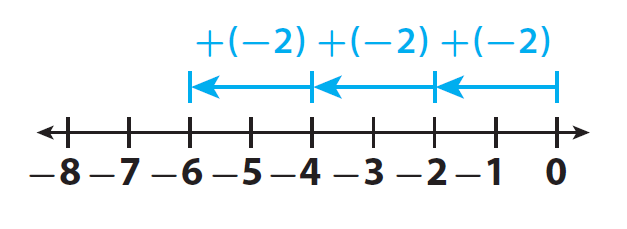
From 0, when we move 2 units to the left 3 times, we get a total move of 6 units. 

The result is -6. 

So, the change in David’s balance was -$6. 

(The negative sign indicates the reduce in balance)

Example 3 : 

Gina hiked down a canyon and stopped each time she descended 1/2 mile to rest. She hiked a total of 4 sections. What is her overall change in elevation?

Solution : 

Step 1 : 

Use a negative number to represent the change in elevation.

Step 2 : 

Find 4 x (-1/2). 

Step 3 : 

Start at 0. Move 1/2 unit to the left 4 times.

The result is -2.

Hence, the overall change is -2 miles. 

Check : 

Use the rules for multiplying rational numbers.

4 x (-1/2) = - 4/2  A negative times a positive equals a the the the the te kdjhnegative.

4 x (-1/2) = - 2      Simplify

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.