MULTIPLYING RATIONAL EXPRESSIONS

Multiply the rational expressions and show the product in simplest form :

Example 1 :

[(x² - 2x)/(2x + 4)] ⋅ [(3x + 6)/(5x - 10)]

Solution :

=  [(x² - 2x)/(2x + 4)] ⋅ [(3x + 6)/(5x - 10)]

Multiply numerators and denominators. 

=  [(x² - 2x)(3x + 6)] /[(2x + 4)(5x - 10)]

Factor the numerator and denominator. 

=  [x(x - 2)3(x + 2)] /[2(x + 2)5(x - 2)]

=  [3x(x - 2)(x + 2)] /[10(x + 2)(x - 2)]

Cancel common factors.  

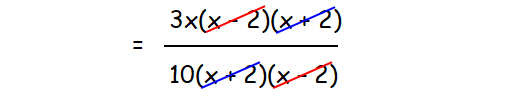
=  3x/10

Example 2 :

[(6x + 6)/(x² - 4)] ⋅ [(x² + 6x + 8)/(3x + 3)]

Solution :

=  [(6x + 6)/(x² - 4)] ⋅ [(x² + 6x + 8)/(3x + 3)]

Multiply numerators and denominators. 

=  [(6x + 6)(x² + 6x + 8)] / [(x² - 4)(3x + 3)]

Factor the numerator and denominator. 

=  [6(x + 1)(x + 2)(x + 4)] / [(x + 4)(x - 4)3(x + 1)]

=  [6(x + 1)(x + 2)(x + 4)] / [3(x + 4)(x - 4)(x + 1)]

Cancel common factors. 

=  [6(x + 2)] / [3(x - 4)]

=  2(x + 2)/(x - 4)

Example 3 :

[(a + b)/(a - b)] ⋅ [(a³ - b³)/(a³ + b³)]

Solution :

=  [(a + b)/(a - b)] ⋅ [(a³ - b³)/(a³ + b³)]

Multiply numerators and denominators. 

=  [(a + b)(a³ - b³)]/[(a - b)(a³ + b³)]

Factor the numerator and denominator. 

=  [(a + b)(a - b)(a² + ab + b²)]/[(a - b)(a + b)(a² - ab + b²)]

Cancel common factors. 

=  (a² + ab + b²) / (a² - ab + b²)

Example 4 :

(5ab/15cd) ⋅ (4bc/32ad) ⋅ (16ac/2bc)

Solution :

=  (5ab/15cd) ⋅ (4bc/32ad) ⋅ (16ac/2bc)

Multiply numerators and denominators. 

=  (5ab ⋅ 4bc ⋅ 16ac) / (15cd ⋅ 32ad ⋅ 2bc)

=  320a²b²c² / 960abc²d²

Cancel common factors. 

=  ab/3d²

Example 5 :

[(x² - 2x + 1)/(x² - 3x + 2)] ⋅ [(3x - 6)/(6x - 6)]

Solution :

=  [(x² - 2x + 1)/(x² - 3x + 2)] ⋅ [(3x - 6)/(6x - 6)]

Multiply numerators and denominators. 

[(x² - 2x + 1)(3x - 6)] / [(x² - 3x + 2)(6x - 6)]

Factor the numerator and denominator. 

=  [(x - 1)(x - 1)3(x - 2)] / [(x - 2)(x - 1)6(x - 1)]

=  [3(x - 1)(x - 1)(x - 2)] / [6(x - 2)(x - 1)(x - 1)]

Cancel common factors. 

=  3/6

=  1/2

Example 6 :

[(x² - 25)/(x + 3)] ⋅ [(x² - 9)/(x + 5)²]

Solution :

=  [(x² - 25)/(x + 3)] ⋅ [(x² - 9)/(x + 5)²]

Multiply numerators and denominators. 

=  [(x² - 25)(x² - 9)] ⋅ [(x + 3)(x + 5)²]

Factor the numerator and denominator. 

=  [(x + 5)(x - 5)(x + 3)(x - 3)] / [(x + 3)(x + 5)(x + 5)]

Cancel common factors. 

=  [(x - 5)(x - 3)] / (x + 5)

Example 7 :

[(x² - 9y²)/(3x - 3y)] ⋅ [(x - y)/(x + 3y)]

Solution :

=  [(x² - 9y²)/(3x - 3y)] ⋅ [(x - y)/(x + 3y)]

Multiply numerators and denominators. 

=  [(x² - 9y²)(x - y)] / [(3x - 3y)(x + 3y)]

Factor the numerator and denominator. 

=  [(x + 3y)(x - 3y)(x - y)] / [3(x - y)(x + 3y)]

Cancel common factors. 

=  (x - 3y)/3

Example 8 :

[(x² - 16)/(x - 2)] ⋅ [(x - 2)/(x³ + 64)]

Solution :

=  [(x² - 16)/(x - 2)] ⋅ [(x - 2)/(x³ + 64)]

Multiply numerators and denominators. 

=  [(x² - 16)(x - 2)] / [(x - 2)(x³ + 64)]

=  [(x² - 4²)(x - 2)] / [(x - 2)(x³ + 4³)]

Factor the numerator and denominator. 

=  [(x + 4)(x - 4)(x - 2)] / [(x - 2)(x + 4)(x² - 4x + 16)]

Cancel common factors. 

=  (x - 4)/(x² - 4x + 16)

Example 9 :

[(p² - 1)/p] ⋅ [p³/(p - 1)] ⋅ [1/(p + 1)]

Solution :

=  [(p² - 1)/p] ⋅ [p³/(p - 1)] ⋅ [1/(p + 1)]

Multiply numerators and denominators. 

=  [(p² - 1) ⋅ p³ ⋅ 1] / [p(p - 1)(p + 1)]

=  p³(p² - 1) / p(p² - 1²)

=  p³(p² - 1) / p(p² - 1)

Cancel common factors. 

=  p²

Example 10 :

[(px - 2p)/(qx - 3q)] ⋅ [(bx - 3b)/(ax - 2a)]

Solution :

=  [(px - 2p)/(qx - 3q)] ⋅ [(bx - 3b)/(ax - 2a)]

Multiply numerators and denominators. 

=  [(px - 2p)(bx - 3b)] / [(qx - 3q)(ax - 2a)]

Factor the numerator and denominator. 

=  [p(x - 2)b(x - 3)] / [q(x - 3)a(x - 2)]

=  [bp(x - 2)(x - 3)] / [aq(x - 3)(x - 2)]

Cancel common factors. 

=  bp/aq

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.