MULTIPLYING POLYNOMIALS BOX METHOD

By using this method we can multiply any two polynomials.

In this method we need to draw a box which contains some rows and columns.

Here, the number of rows is up to the number of terms of the first polynomial and the number of columns is up to the number of terms of the second polynomial.

Example 1 :

Multiply the following polynomials using box method.

(2x + 8) and (6x + 2)

Solution :

Here we use box method to multiply the above polynomials.

The 1^st and 2^nd polynomial is containing two terms, so the number of rows and number of columns in the box must be 2.

Step 1 :

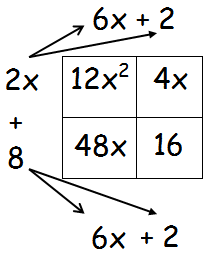
Step 2 :

Combining the terms

  =  12x² + 4x + 48x + 16

  =  12x² + 52x + 16

Example 2 :

Multiply the following polynomials using box method.

(2x - 3) and (3x + 5)

Solution :

Here we use box method to multiply the above polynomials.

The 1^st and 2^nd polynomial is containing two terms, so the number of rows and number of columns in the box must be 2.

Step 1 :

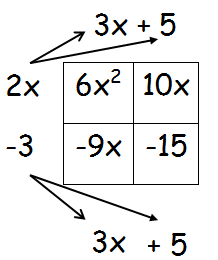
Step 2 :

Combining the terms

  =  6x² + 10x -9x - 15

  =  6x² + x - 15

Example 3 :

Multiply the following polynomials using box method.

2x and (6x² - 9xy + y²)

Solution :

Here we use box method to multiply the above polynomials.

In the box, 

Number of rows = 1

Number of columns = 3

Step 1 :

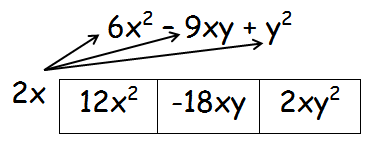
Step 2 :

We don't have any like terms

  =  12x² - 18xy + 2xy²

Hence the product of the above binomials is 12x² - 18xy + 2xy²

Example 4 :

Multiply the following polynomials using box method.

(7x - 3) and (x² - 2x + 7)

Solution :

Here we use box method to multiply the above polynomials.

In the box, 

Number of rows = 2

Number of columns = 3

Step 1 :

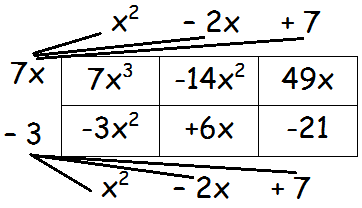
Step 2 :

Combining the like terms

  =  7x³ - 14x² - 3x² + 49x + 6x - 21

  =  7x³ - 17x² + 55x - 21

Example 5 :

Multiply the following polynomials using box method.

(4x + 2) and (6x² - x + 2)

Solution :

Here we use box method to multiply the above polynomials.

In the box, 

Number of rows = 2

Number of columns = 3

Step 1 :

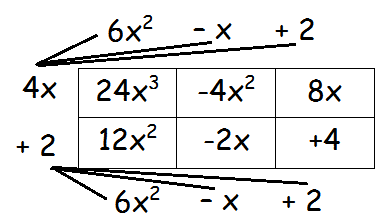
Step 2 :

Combining the like terms

  =  24x³ - 4x² +12x² + 8x - 2x + 4

  =  24x³ + 8x² + 6x + 4

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.