MODULAR ARITHMETIC

In a clock, we use the numbers 1 to 12 to represent the time period of 24 hours. How is it possible to represent the 24 hours of a day in a 12 number format? We use 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 and after 12, we use 1 instead of 13 and 2 instead of 14 and so on. That is after 12 we again start from 1, 2, 3,...

In this system the numbers wrap around 1 to 12. This type of wrapping around after hitting some value is called Modular Arithmetic.

In Mathematics, modular arithmetic is a system of arithmetic for integers where numbers wrap around a certain value. Unlike normal arithmetic, Modular Arithmetic process cyclically. The ideas of Modular arithmetic was developed by great German mathematician Carl Friedrich Gauss, who is hailed as the “Prince of mathematicians”.

Examples :

1. The day and night change repeatedly.

2. The days of a week occur cyclically from Sunday to Saturday.

3. The life cycle of a plant.

4. The seasons of a year change cyclically. (Summer, Autumn, Winter, Spring).

When we divide two integers, say 'X' and 'Y', we will have an equation that looks like the following :

X/Y = Q remainder R

Here,

X is the dividend

Y is the divisor

Q is the quotient

R is the remainder

Sometimes, we would be interested to know only the remainder when X is divided by Y.

For such cases, the operator called modulo (abbreviated as mod) will be used.

Using the same X, Y, Q and R as above, we can have

X mod Y = R

We say this as X modulo Y is equal to R, where Y is referred to as the modulus.

For example,

18/7 = 2 remainder 4

18 mod 7 = 4

Visualizing Modulus with Clocks

Observe what happens when a number is increased by one and divided by 4.

0/4 = 0 remainder 0

1/4 = 0 remainder 1

2/4 = 0 remainder 2

3/4 = 0 remainder 3

4/4 = 1 remainder 0

5/4 = 1 remainder 1

6/4 = 1 remainder 2

7/4 = 1 remainder 3

8/4 = 2 remainder 0

The remainder starts at 0 and it increases by 1 each time, until the number reaches one less than the number we are dividing by. After that, the sequence repeats.

Observing this, we can visualize the operator modulo using circles.

We write 0 at the top of the circle and continue clockwise writing integers 1, 2,........ up to one less than the modulus.

For example a clock with the 12 replaced by a 0 would be the circle for a modulus of 12.

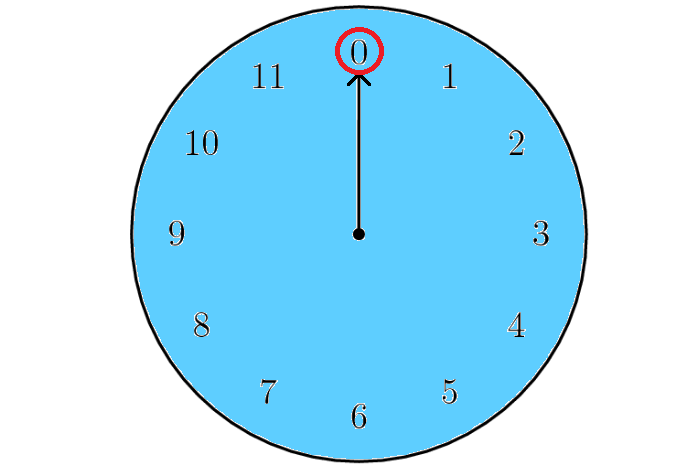
To find the result of X mod Y, we can do the following steps.

Step 1 :

Construct this clock for size Y.

Step 2 :

Start at 0 and move around the clock X steps.

Step 3 :

Wherever we land is our solution.

(If the number is positive, we step clockwise, if it's negative, we step counter-clockwise.)

Example 1 :

Compute :

8 mod 4

Solution :

8 is greater than 4.

When 8 is divided by 4, the remainder is 0.

8/4 = (2x4) + 0

So,

8 mod 4 = 0

Example 2 :

Compute :

14 mod 3

Solution :

14 is greater than 3.

When 14 is divided by 3, the remainder is 2.

14/3 = (4x3) + 2

So,

14 mod 3 = 2

Example 3 :

Compute :

3 mod 7

Solution :

3 is less than 7.

3/7 = (0x7) + 3

So,

3 mod 7 = 3

Example 4 :

Compute :

-5 mod 2

Solution :

Here, the dividend is -5 (negative number) and 5 is not divisible by the divisor 2. Now, we have to find the number which comes after 5 that is evenly divisible by the divisor 2. That is 6.

So, we have to write -5 in terms -6.

-5 = -6 + 1

Therefore,

-5 mod 2 = 1

Example 5 :

Compute :

-4 mod 2

Solution :

Here, the dividend is -4 (negative number) and 4 is evenly divisible by the divisor 2.

So,

-4 mod 2 = 0

Example 6 :

Compute :

-11 mod 5

Solution :

Here, the dividend is -11 (negative number) and 11 is not divisible by the divisor 5. Now, we have to find the number which comes after 11 that is evenly divisible by the divisor 5. That is 15.

So, we have to write -11 in terms -15.

-11 = -15 + 4

Therefore,

-11 mod 5 = 4

Example 7 :

Compute :

-12 mod 4

Solution :

Here, the dividend is -12 (negative number) and 12 is evenly divisible by the divisor 4.

So,

-12 mod 4 = 0

Example 8 :

Compute :

-3 mod 5

Solution :

Here, the dividend is -3 (negative number) and 3 is less than the divisor 5. Now, we have to find the number which comes after 3 that is evenly divisible by the divisor 5. That is 5.

So, we have to write -3 in terms -5.

-3 = -5 + 2

Therefore,

-3 mod 5 = 2

MODULAR ARITHMETIC

Visualizing Modulus with Clocks

Related Topics

Recent Articles

Problems on Special Right Triangles

Practice Problems Using Special Right Triangles

How to Find the Missing Value in Composition of Two Functions