VOLUME OF PRISM WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
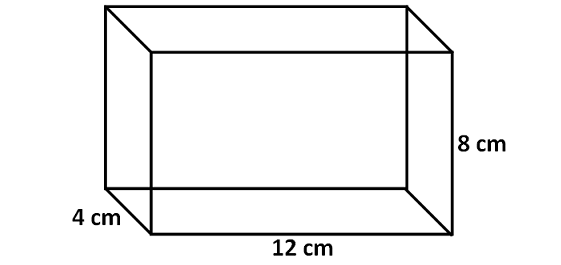
Find the volume of the cuboid shown below.
Problem 2 :
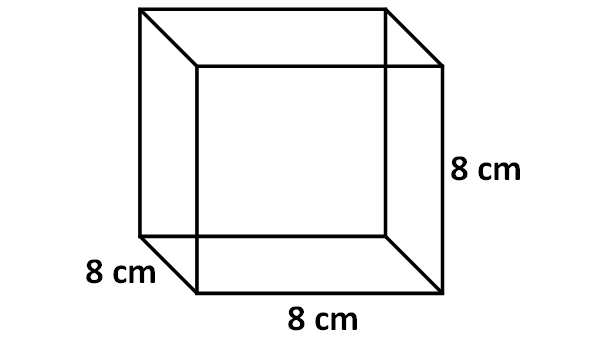
Find the volume of the cube shown below.
Problem 3 :
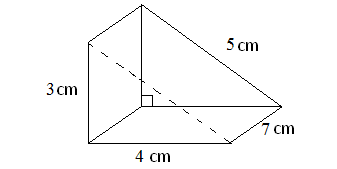
Find the volume of the triangular prism given below.
Problem 4 :
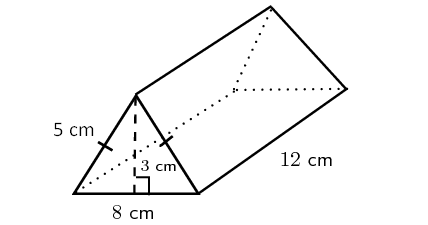
Find the volume of the triangular prism shown below.
Problem 5 :
Find the volume of the triangular prism shown below.
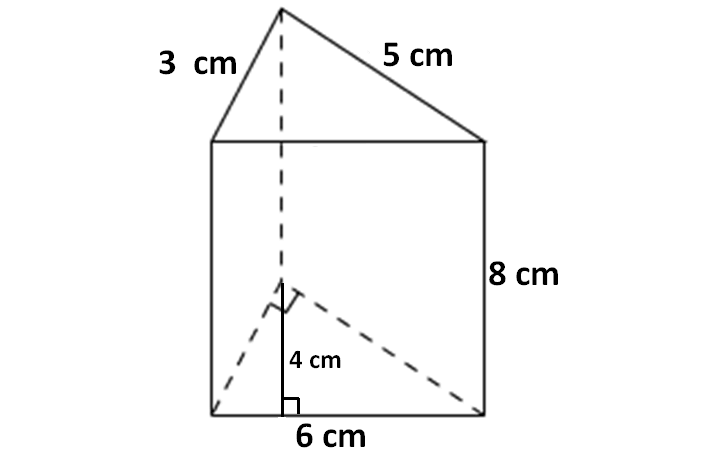
Problem 6 :
Find the volume of the pyramid shown below.
Problem 7 :
Shown below is a prism. The cross-sectional area is 21 cm². The prism has a length of 6 cm.
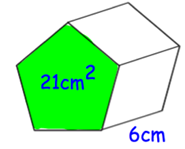
Find the volume of the prism.
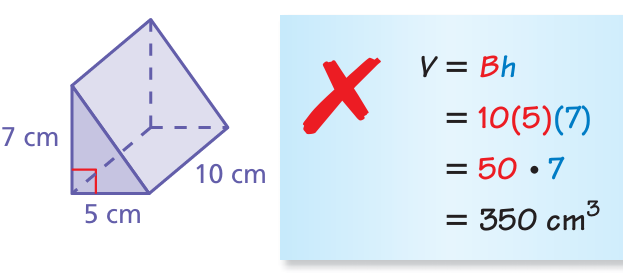
Problem 8 :
Describe and correct the error in finding the volume of the triangular prism.
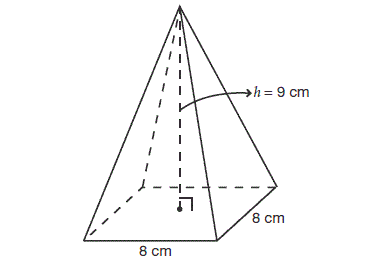
Problem 9 :
As a gift, you fill the calendar with packets of chocolate candy. Each packet has a volume of 2 cubic inches. Find the maximum number of packets you can fi t inside the calendar.

Problem 10 :
Two liters of water are poured into an empty vase shaped like an octagonal prism. The base area is 100 square centimeters. What is the height of the water? (1 L = 1000 cm3)

1. Answer :

Here, the base is a rectangle and all the side walls are also rectangles.
Then, formula for volume of the above cuboid is
= Base Area x Height
Here, the base is a rectangle with length 12 cm and width 4 cm.
Area of base is
= 12 x 4 = 48 cm2
Height of the cuboid is 8 cm.
So, volume of the above cuboid is
= 48 x 8
= 384 cm3
2. Answer :

Here, the base is a square and all the side walls are also squares.
Then, formula for volume of the above cube is
= Base area x Height
Here, the base is a square with side length of 8 cm.
Area of base is
= 8 x 8
= 64 cm2
Height of the cube is 8 cm.
So, volume of the above cube is
= 64 x 8
= 512 cm3
3. Answer :

Here, the base is a rectangle, two of the side walls are triangles and other two side walls are rectangles.
Then, formula for the above triangular prism is
= (1/2) x Base area x Height
Here, the base is a rectangle with length 7 cm and width is 4 cm.
So, area of the base is
= 7 x 4
= 28 cm2
Height of the prism is 3 cm.
So, volume of the above triangular prism is
= (1/2) x 28 x 3
= 42 cm3
4. Answer :

Here, the base is a rectangle, two of the side walls are triangles and other two side walls are rectangles.
Then, formula for the above triangular prism is
= (1/2) x Base area x Height
Here, the base is a rectangle with length 12 cm and width is 8 cm.
So, area of the base is
= 12 x 8
= 96 cm2
Height of the prism is 3 cm.
So, volume of the above triangular prism is
= (1/2) x 96 x 3
= 144 cm3
5. Answer :

Here, the base is a triangle, and all the side walls are rectangles.
Then, formula for the above triangular prism is
= Base area x Height
Here, the base is a triangle with base 6 cm and height 4 cm.
So, area of the base is
= (1/2) x 6 x 4
= 12 cm2
Height of the prism is 8 cm.
So, volume of the above triangular prism is
= 12 x 8
= 96 cm3
6. Answer :

Here, the base is a square, and all the side walls are triangles.
Then, formula for the above triangular prism is
= (1/3) x Base area x Height
Here, the base is a square with side length 8 cm.
So, area of the base is
= 8 x 8
= 64 cm2
Height of the pyramid is 9 cm.
So, volume of the above triangular prism is
= (1/3) x 64 x 9
= 192 cm3
7. Answer :

Base area of pentagon = 21 cm2
Height = 6 cm
Volume of pentagon shaped prism = base area x height
= 21 x 6
= 126 cm3
8. Answer :

In the given triangular base prism, the base is in the shape of right triangle
Base area = (1/2) x base x height
= (1/2) x 5 x 7
= 35/2
= 17.5 cm2
Height = 10 cm
Volume of the triangular prism = base area x height
= 17.5 x 10
= 175 cm3
9. Answer :

Volume of calender = (1/2) x base x height of triangle x height of prism
= (1/2) x 4 x 6 x 8
= 2 x 6 x 8
= 96 cubic inches
Volume of each packet = 2 cubic inches
Number of packets to be filled = 96/2
= 48 packets.
10. Answer :
1 liter = 1000 cm3
2 liter = 2000 cm3
Capacity of octagonal prism = base area x height
2000 = 100 x h
2000/100 = h
h = 20 cm
So, the required height of the octagonal prism is 20 cm.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
90 Degree Clockwise Rotation
Jan 01, 26 06:58 AM
90 Degree Clockwise Rotation - Rule - Examples with step by step explanation -
US Common Core K-12 Curriculum Algebra Solving Systems of Equations
Jan 01, 26 04:51 AM
US Common Core K-12 Curriculum - Algebra : Solving Systems of Linear Equations -
Solving the HARDEST SAT Math Questions ONLY using Desmos
Dec 31, 25 05:53 AM
Solving the HARDEST SAT Math Questions ONLY using Desmos
