MODELING THE VOLUME OF A SPHERE

A sphere is a three-dimensional figure where all the points on the sphere would be at the same distance from the center. The radius of a sphere is the distance between the center to any point on the sphere.

Modeling the Volume of a Sphere

We already know that a cone can fill one-third of a cylinder of where the radius and height of the cone and cylinder would be same. 

If we do a similar experiment with a sphere of the same radius that the cylinder has, we will find that the sphere can fill two-third of the cylinder.

Here, the cylinder’s height would be equal to two times the the radius of the sphere.

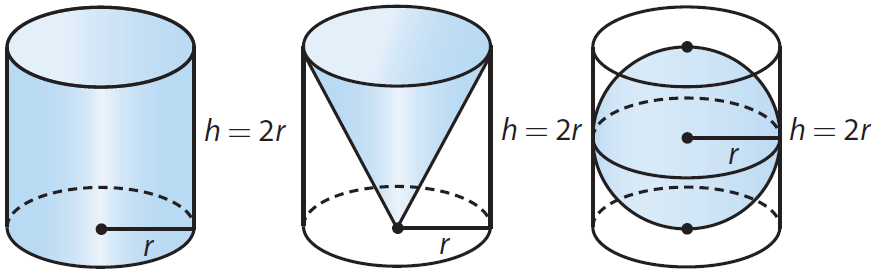
Step 1 :

Write the formula for volume V of a cylinder with base area B and height h.

V = B · h

Step 2 :

Find the base area B of the cylinder.

We know that the base of the cylinder is a circle (Look at the figure given below).

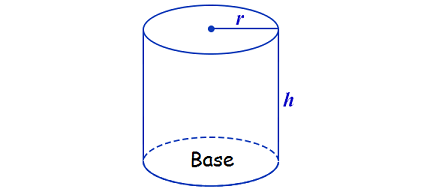
So, the area of the base of a cylinder is

B = πr²

Step 3 :

Write the formula for volume V of a cylinder with base area B = πr² and height h.

V = πr²h

Step 4 :

A sphere of the same radius that the cylinder has, we will find that the sphere can fill two-third of the cylinder.

So, we have

Volume of sphere = 2/3 · Volume of cylinder 

Volume of sphere = 2/3 · πr²h

(Here, radius and height of the sphere and radius and height of the cylinder are equal)

Step 5 :

A sphere always has a height which is equal to twice the radius.

So, substitute 2r for h.

Volume of sphere = 2/3 · πr²(2r)

Simplify.

Volume of sphere = 4/3 · πr³ cubic units

Reflect

A cone has a radius of r and a height of 2r. A sphere has a radius of r. Compare the volume of the sphere and cone.

The cone’s volume is one-third of a cylinder with radius r and height 2r. The sphere’s volume is two-third of the volume of this cylinder. So, the sphere’s volume is twice the cone’s volume.

Problem 1 :

A solid sphere of radius r is melted and recast into the shape of a solid cone of height r. Find the radius of the base of the cone.

Solution :

Sphere :

Radius = r

Cone :

Radius = r and height = h

Volume of sphere = volume of cone

(4/3) · πr³ = (1/3) · πr²h

4r = h

r = h/4

So, the radius of the cone is h/4.

Problem 2 :

If the ratio of volume of two spheres is 1 : 8, then find the ratio of their surface area.

Solution :

Let r₁ and r₂ be the radii of two spheres.

Ratio between volumes = 1 : 8

(4/3) πr₁³ : (4/3) πr₂³ = 1 : 8

r₁³ : r₂³ = 1 : 8

r₁³ : r₂³ = 1³ : 2³

r₁ : r₂ = 1 : 2

r₂: 2r₁

Ratio between surface area of spheres = 4 πr₁² : 4 πr₂²

= r₁² : (2r₁)²

= r₁² : 4r₁²

= 1 : 4

Problem 3 :

Volumes of two spheres are in the ratio 27 : 64. The ratio of their surface areas is :

(a) 3 : 4     (b) 4 : 3    (c) 9 : 16    (d) 16 : 9

Solution :

Ratios of volumes of two spheres =  27 : 64

(4/3) πr₁³ : (4/3) πr₂³ = 27 : 64

r₁³ : r₂³ : 27 : 64

r₁³ : r₂³ : 3³ : 4³

r₁ : r₂ = 3 : 4

r₁  = (3/4)r₂

Ratio between surface area of spheres = 4 πr₁² : 4 πr₂²

= (3/4r₂)² : r₂²

= (3/4)² : 1

= 9 : 16

So, the ratio between the surface areas is 9 : 16.

Problem 4 :

A metallic spherical shell of internal and external diameters 4 cm and 8 cm respectively is melted and recast into the form of a cone of base diameter 8 cm. Find height of the cone.

Solution :

Volume of hollow sphere = (4/3) π(R³ - r³)

External radius (R) = 4 cm, internal radius (r) = 2 cm

= (4/3) π(R³ - r³)

= (4/3) π(4³ - 2³)

= (4/3) π(64 - 8)

= (4/3) x π x 56 -----(1)

Volume of cone =  (1/3) πr²h

Radius of cone = 4 cm

= (1/3) π(4)²h

= (1/3) π x 16 x h -----(2)

Volume of sphere = volume of cone

(4/3) x π x 56 = (1/3) π x 16 x h

4 x 56 = 16 x h

h = (4 x 56)/16

h = 14

So, the height of the cone is 17 cm.

Problem 5 :

If the volume of a sphere is 288π cm³, the radius is __________ cm.

Solution :

Volume of sphere =  288π cm³

(4/3) πr³ = 288π

(4/3) r³ = 288

r³ = 288 x (3/4)

r³ = 216

r³ = 6³

r = 6

So, the radius of the sphere is 6 cm.

Problem 6 :

A toy is in the form of a hemisphere surmounted by a right circular cone of the same base radius as that of the hemisphere. If the radius of base of the cone is 21 cm and its volume is 2/3 of the volume of the hemisphere, calculate the height of the cone and the surface area of the toy. [Use = 22/7 ]

Solution :

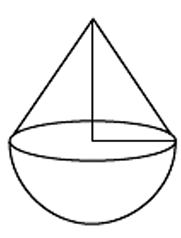
Volume of cone = 2/3 volume of hemisphere

(1/3) πr² h = 2/3 of ((2/3) πr³)

(1/3) πr² h = (4/9) πr³

h = (4/3)r

Applying r = 21 cm, we get 

h = (4/3)(21)

= 28 cm

So, height of the cone is 28 cm.

Surface area of the toy = πrl + 2 πr²

= πr(l + r)

slant height (l) = √(21² + 28²)

= √(441 + 784)

= √1225

= 35 cm

Applying the value of l, we get

= (22/7) x 21(35 + 21)

= 22 x 3 x 56

= 3696 cm²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.