MODELING THE VOLUME OF A CYLINDER

A cylinder is a three-dimensional figure that has two congruent circular bases that lie in parallel planes. The volume of any three-dimensional figure is the number of cubic units needed to fill the space taken up by the solid figure.

Modeling the Volume of a Cylinder

One cube represents one cubic unit of volume. We can develop the formula for the volume of a cylinder using an empty soup can or other cylindrical container. First, remove one of the bases. 

Step 1 :

Arrange centimeter cubes in a single layer at the bottom of the cylinder as shown in the figure. Fit as many cubes into the layer as possible.

Step 2 :

To find how many layers of cubes fit in the cylinder, make a stack of cubes along the inside of the cylinder as shown in the figure. 

Step 3 :

To find the approximate number of cubes that would fit in the cylinder, multiply the number of cubes in the bottom layer times the number of layers.

Now, the approximate volume of the cylinder is the total number of cubes in the cylinder.

Reflect

1. Suppose you know the area of the base of a cylinder and the height of the cylinder. How can you find the cylinder’s volume ?

Multiply the area of the base times the height.

2. Let the area of the base of a cylinder be B and the height of the cylinder be h. Write a formula for the cylinder’s volume V.

V = Bh

The base of a cylinder is a circle, so for a cylinder,

B = πr²

Then, we have

V = πr²h cubic units

Solved Problems

Problem 1 :

Find the volume of the cylinder given below. Round your answer to the nearest tenth if necessary. Use the approximate of value of π, that is 3.14. 

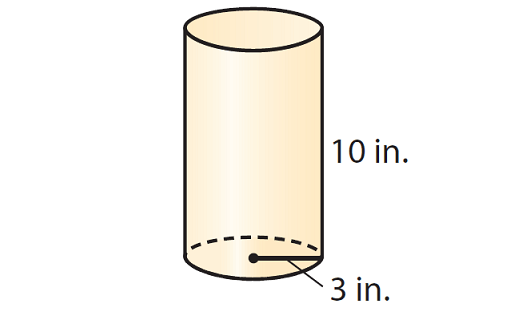
Solution :

Step 1 :

Write the formula to find volume of a cylinder

V = πr²h cubic units

Step 2 :

Substitute the given measures.

V ≈ 3.14 · 3² · 10

Simplify.

V ≈ 3.14 · 9 · 10

V ≈ 282.6

So, the volume of the given cylinder is about 282.6 cubic inches.

Problem 2 :

Find the volume of the cylinder given below. Round your answer to the nearest tenth if necessary. Use the approximate of value of π, that is 3.14.

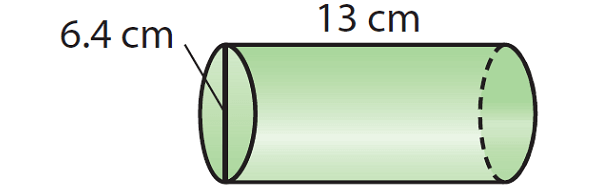
Solution :

Step 1 :

Write the formula to find volume of a cylinder

V = πr²h cubic units

Step 2 :

To find the volume, we need the radius of the cylinder. But, the diameter is given, that is 6.4 cm. So, find the radius.

r = diameter/2

r = 6.4/2

r = 3.2

Step 3 :

The given cylinder is in horizontal position and its length is 13 cm. If the cylinder is in vertical position, the length will become height. So, the height is

h = 13

Step 4 :

Substitute r = 3.2 and h = 13.

V ≈ 3.14 · (3.2)² · 13

Simplify.

V ≈ 3.14 · 10.24 · 13

V ≈ 418

So, the volume of the given cylinder is about 418 cubic cm.

Problem 3 :

You are melting a rectangular block of wax to make candles. How many candles of the given shape can be made using a block that measures 10 centimeters by 9 centimeters by 20 centimeters?

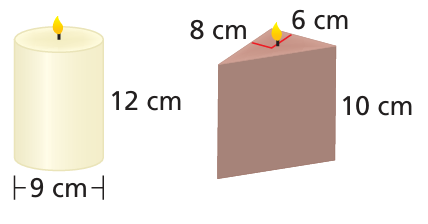
Solution :

Measurements of rectangular block :

length = 10 cm, width = 9 cm and height = 20 cm

Measurements of triangular prism shape candle :

Base of triangle = 6, height = 8cm and height of prism = 10 cm

Measurements of cylindrical shaped candle :

radius = 9/2 ==> 4.5 cm

height = 12 cm

Number of cylindrical shape candles can be made :

= Volume of rectangular prism / volume of cylinder

= 10 x 9 x 20 / π x 4.5² x 12

= 1800 / (3.14 x 20.25 x 12)

= 1800/763.02

= 2.35

Approximately 2 candles can be made.

Number of cylindrical shape candles can be made :

= Volume of rectangular prism / volume of triangular prism

= 10 x 9 x 20 / 0.5 x 8 x 6 x 10

= 9 x 20 / 0.5 x 8 x 6

= 7.5

Approximately 7 candles can be made.

Problem 4 :

Water flows at 2 feet per second through a pipe with a diameter of 8 inches. A cylindrical tank with a diameter of 15 feet and a height of 6 feet collects the water.

a. What is the volume, in cubic inches, of water flowing out of the pipe every second?

b. What is the height, in inches, of the water in the tank after 5 minutes?

c. How many minutes will it take to fill 75% of the tank?

Solution :

a)  Speed of leakage = 2 feet per second

radius = 4 inches

2 feet = 12 inches

converting into cubic inches, we get

= 12³

= 1728 cubic inches

Quantity of water leakage per second = π r² x speed

= 3.14 x 4² x 1728

= 86814.72 cubic inches every second.

b)  1 minute = 60 seconds

5 minutes = 300 seconds

= 300 x 86814.72

= 361728

c) Capacity of the tank 

radius = 7.5 feet ==> 90 inches

height = 6 feet ==> 72 inches

= 3.14 x 90² x 72

= 1831248

75% of 1059.75 = 0.75(1831248)

= 1373436 cubic feet

Time tanken = 1373436 / 86814.72

= 15.8

Approimately 16 seconds.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.