MODELING THE VOLUME OF A CONE

A cone is a three-dimensional figure that has one vertex and one circular base as shown in the figure given below.

Let us see how the volume of a cone can be modeled. 

To explore the volume of a cone, Alexa does an experiment with a cone and a cylinder that have congruent bases and heights. She fills the cone with popcorn kernels and then pours the kernels into the cylinder as shown in the figure.

She repeats this until the cylinder is full.

Alexa finds that it takes 3 cones to fill the volume of the cylinder.

Step 1 :

Write the formula for volume V of a cylinder with base area B and height h.

V = B · h

Step 2 :

Find the base area B of the cone. 

We know that the base of the cone is a circle (Look at the figure given below).  

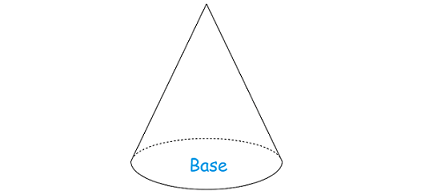
So, the area of the base of a cone is 

B = πr²

Step 3 :

Alexa found that, when the bases and height are the same,

3 x Volume of cone = Volume of cylinder

Step 4 :

From step 3, solve for volume of cone. 

3 x Volume of cone = Volume of cylinder

Divide both sides by 3. 

(3 x Volume of cone) ÷ 3 = Volume of cylinder ÷ 3

Volume of cone = 1/3 · Volume of cylinder

(Here, base radius and height of the cone and base radius and height of the cylinder are equal)

The formula to find the volume of a cone is given by

V = 1/3 · πr²h cubic units

Reflect

1. Use the conclusion from this experiment to write a formula for the volume of a cone in terms of the height and the radius. Explain.

Volume of the cone = 1/3 · Volume of cylinder

Substitute the formula for volume of cylinder.

Volume of the cone = 1/3 · πr²h

2. How do you think the formula for the volume of a cone is similar to the formula for the volume of a pyramid ?

Both are one third the area of the base times the height.

Problem 1 :

You must answer a trivia question before the sand in the timer falls to the bottom. The sand falls at a rate of 50 cubic millimeters per second. How much time do you have to answer the question?

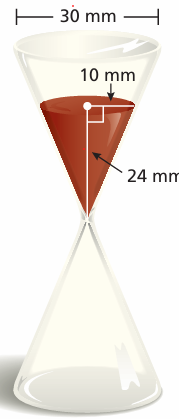
Solution :

Volume of sand in the timer = 1/3 · πr²h

radius (r) = 10 mm, height (h) = 24 mm

= 1/3 · (3.14)(10)²(24)

= 2512 mm³

Speed of sand fall = 50 cubic mm per second

Total time taken = 2512 / 50

= 50.24

So, you have about 50 seconds to answer the question.

Problem 2 :

The volume of a cone is 20 π cubic meters. What is the volume of a cylinder with the same base and height?

Solution :

Volume of cone =  20 π cubic meters

(1/3) · πr²h = 20 π

πr²h = 20 π(3)

πr²h = 60 π

So, the volume of cylinder is 60 π.

Problem 3 :

Water leaks from a crack in a vase at a rate of 0.5 cubic inch per minute. How long does it take for 20% of the water to leak from a full vase?

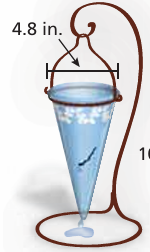
Solution :

Radius = 4.8/2 ==> 2.4 inches

height = 1 inch

Capacity of the vase = (1/3) · πr²h

= (1/3) · 3.14 (2.4)²(1)

= 6.0288

20% of capacity of the vase = 20% of 6.0288

= 0.20(6.0288)

= 1.20576 cubic inches

Leakage = 0.5 cubic inches

Time taken = 1.20576/0.5

= 2.41 minutes

Problem 4 :

You have 10 gallons of lemonade to sell. (1 gal ≈ 3785 cm³)

a. Each customer uses one paper cup. How many paper cups will you need?

b. The cups are sold in packages of 50. How many packages should you buy?

c. How many cups will be left over if you sell 80% of the lemonade?

Solution :

Quantity of lemonade you have = 10 gallons

1 gal = 3785 cm³

10 gallons = 37850 cm³

Capacity of paper cup = (1/3) · πr²h

r = 4 cm and h = 11 cm

= (1/3) · π (4)²(11)

= 58.66 x 3.14

= 184.21 cm³

a) Number of paper cups needed = 37850/184.21

= 205.4

Approximately 206 cups are needed.

b)

Number of cups in one package = 50

Number of package needed = 206/50

= 4.12

approximately 5 packages are needed.

c)

80% of 37850

= 0.80(37850)

= 30280

Capacity of one cup = 184.21

Number of cups to be filled with 80% of lemonade 

= 30280/184.21

= 164.3

approximately 165 cups

5 package = 250 cups

= 250 - 165

= 85 cups will be left over.

Problem 5 :

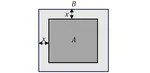
The cylinder and the cone have the same volume. What is the height of the cone?

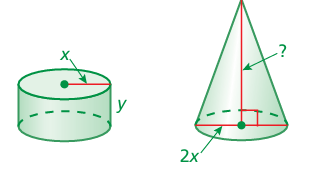
Solution :

Volume of cylinder = volume of cone

 πr²h = (1/3) · πr²h

Radius of cone = 2x/2 ==> x

x²y = (1/3) · x²h

y = (1/3) h

h = 3y

So, height of the cone is 3y.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.