MODELING FRACTION DIVISION

For some real-world problems, we may need to divide a fraction by a fraction. Sometimes, we may need to divide a fraction by a whole number.

Example 1 : 

David has 3/4 cup of salsa for making burritos. Each burrito requires 1/8 cup of salsa. How many burritos can David make ?

Solution : 

To find the number of burritos that can be made, you need to determine how many 1/8 -cup servings are in 3/4 cup.

In the diagram given below, 3/4 of a whole is divided into quarters and into eighths.

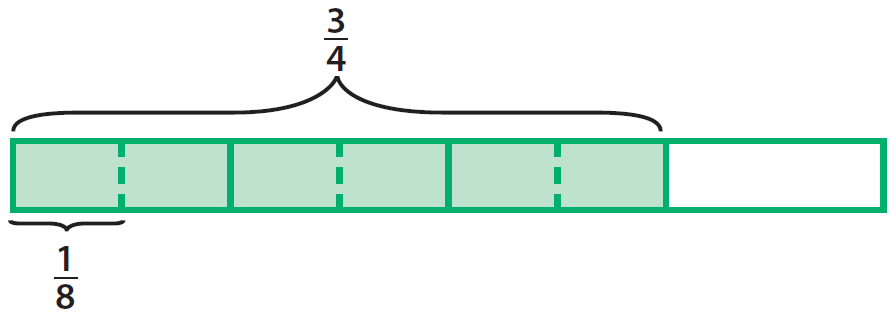
In the whole cup, there are eight 1/8 cups.

But, David has 3/4 cup of salsa.

So, we have to count the number of 1/8 cups in 3/4 cup in the above diagram. 

And there are six 1/8 cups in 3/4 cup of salsa. 

Hence, David can make 6 burritos from 3/4 cup of salsa.

Example 2 : 

Five people share 1/2 pound of cheese equally. How much cheese does each person receive?

Solution : 

To find how much cheese each person receives, you can divide 1/2 pound into 5 equal parts. Use the diagram to determine what fraction of a whole pound each person receives.

In the diagram given below, 1/2 of a whole is divided into halves and into tenths.

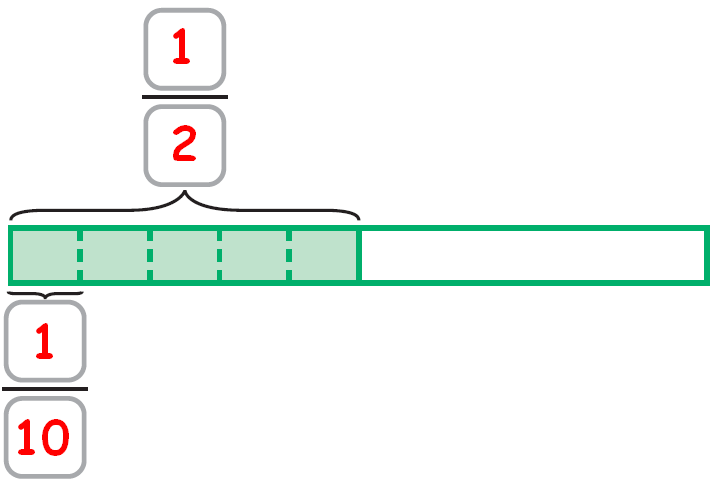
In one pound of cheese, there are ten 1/10s.

But, there is 1/2 pound of cheese.

So, we have to count the number of 1/10s in 1/2 pound of cheese.  

And there are five 1/10s in 1/2 pound of cheese. 

Hence, Each person will receive 1/10 pound of cheese. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.