MODELING EQUATIONS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
An equation is a mathematical statement that two expressions are equal. An equation may or may not contain variables. For an equation that contains a variable, a solution of the equation is a value of the variable that makes the equation true.
Example 1 :
A puppy weighed 6 ounces at birth. After two weeks, the puppy weighed 14 ounces. Represent the given situation as an equation.
Model the equation and find how much weight that puppy gained.
Solution :
Write a word equation based on the situation.

Rewrite the equation using a variable for the unknown quantity and the given values for the known quantities.
Let x represent the number of ounces gained.
Then, we have
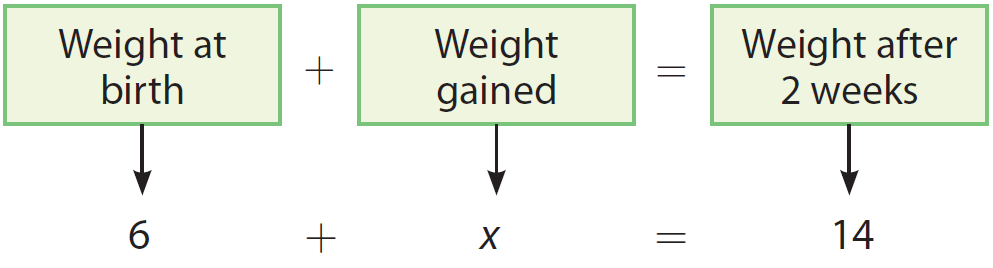
Therefore, the equation '6 + x = 14' represents the given situation.
Let us model the equation '6 + x = 14' using algebra tiles.
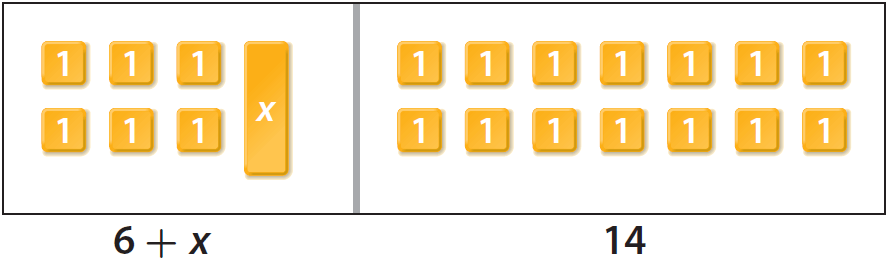
To find how much weight that puppy gained, we have to solve for x.
To solve for x in the above model, we have to isolate x.
That is, we have to remove six 1 tiles on the left side.
Whenever we remove tiles from one side of the mat, we must remove the same number of tiles from the other side of the mat.
Cross out six 1 tiles on the left side and do the same on the other side.
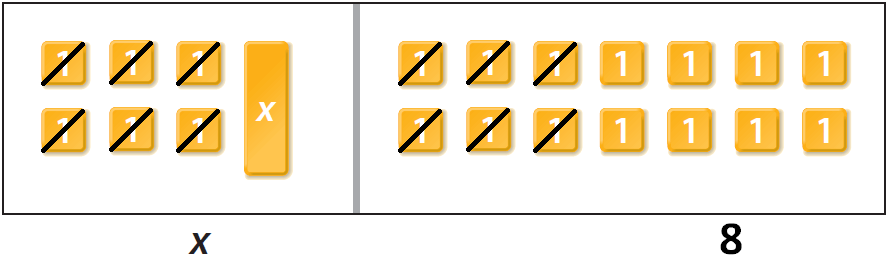
In the above model, we find x on the left side and eight 1 tiles on the right side.
So, the value of x is 8.
Hence, the puppy gained 8 ounces of weight.
Example 2 :
Sarah used a gift card to buy $3 worth of food. She has $2 left on her gift card. Write an equation to represent this situation.
Model the equation and find how much money that she had initially in her gift card.
Solution :
Write a word equation based on the situation.

Rewrite the equation using a variable for the unknown quantity and the given values for the known quantities.
Let x be the amount on the card.
Then, we have
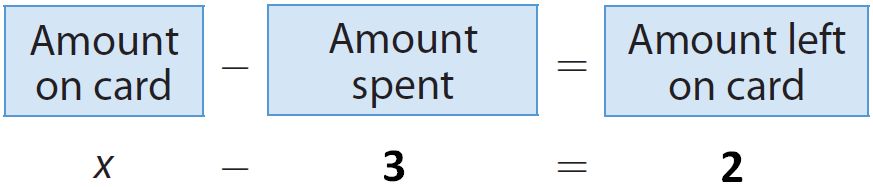
Therefore, the equation 'x - 3 = 2' represents the given situation.
Let us model the equation 'x - 3 = 2' using algebra tiles.
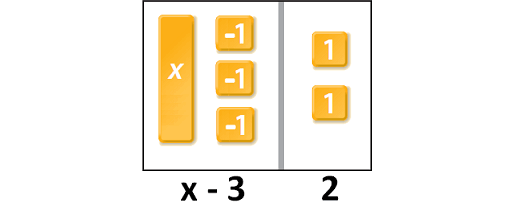
To find how much money that Sarah had initially, we have to solve for x.
To solve for x in the above model, we have to isolate x.
That is, we have to remove six -1 tiles on the left side.
Whenever we remove -1 tiles from one side of the mat, we must add the same number of 1 tiles on both sides.
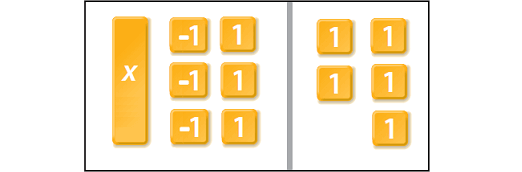
Cross out one -1 tile for one 1 tile.
Then, we have
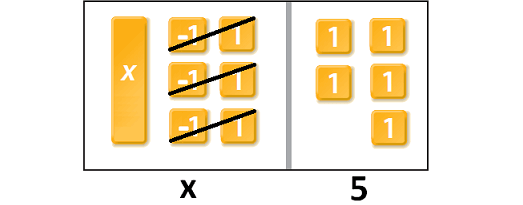
In the above model, we find x on the left side and five 1 tiles on the right side.
So, the value of x is 5.
Hence, Sarah had $5 initially in her gift card.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 06, 26 04:54 AM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4) -
10 Hard SAT Math Questions (Part - 3)
Jan 05, 26 06:34 PM
10 Hard SAT Math Questions (Part - 3)

