MODELING DECIMAL FRACTION AND PERCENT EQUIVALENTS

Using models can help us to understand how decimals, fractions, and percent are related.

Example 1 :

Model 0.78 by shading a 10-by-10 grid.

Solution :

Since there are two digits after the decimal point in 0.78, we can write 0.78 as a fraction 78/100.

0.78 = 78/100

0.78 = 78%

0.78 = 78 out of a hundred

In 10 by- 10 grid, there will be 100 equal parts.

Because 10 x 10 = 100.

Since 0.78 = 78 out of a hundred, we have to shade 78 out 100 parts in 10 by- 10 grid to model the decimal 0.78.

Example 2 :

Model 1.42 by shading a 10-by-10 grid.

Solution :

There are two digits after the decimal point in 1.42. So, we can write 1.42 as a fraction 142/100.

Here, the numerator 142 is greater than 100.

Since we are going to use 10 by 10- grid (100 equal parts), we can write the given decimal 1.42 as given below.

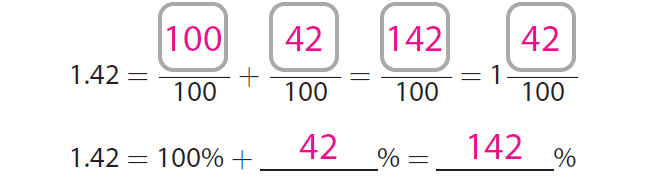
1.42 can be written as shown below.

1.42 = 1 42/100

1.42 = 1 + 42/100

Therefore, there are two parts in 1.42.

They are 1 and 42/100.

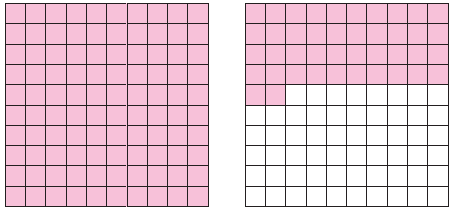
So, we have to use two 10 by-10 grids to model the decimal 1.42.

Since we write 1.42 = 100/100 + 42/100, we have to shade all the 100 parts in the first grid and 42 parts in the second grid.

Example 3 :

Model 125% by shading a 10-by-10 grid.

Solution :

Percent means per hundred.

125% = 125/100

Here, the numerator 125 is greater than 100.

Since we are going to use 10 by 10- grid (100 equal parts), we can write 125% as given below.

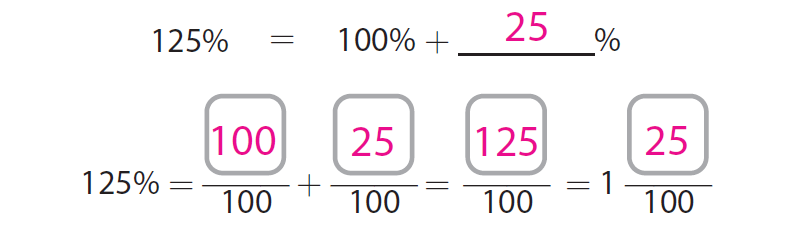
125% can be written as shown below.

125% = 125/100

125% = 1.25

125% = 1 25/100

125% = 1 + 25/100

Therefore, there are two parts in 125%.

They are 1 and 25/100.

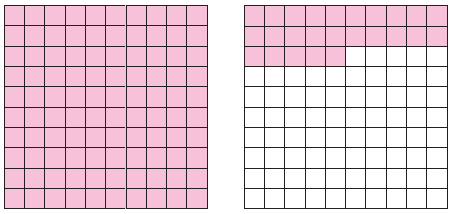
So, we have to use two 10 by-10 grids to model 125%.

Since we write 125%  =  100/100 + 25/100, we have to shade all the 100 parts in the first grid and 25 parts in the second grid.

Example 4 :

a) What fraction of the array of counters is red ?

b) What fraction of the array of counters is yellow ?

c) What percentage of array of counters is red ?

d) What percentage of the array counters is yellow ?

e) What do you notice about the two percentages ?

Solution :

In the array above, 

number of counters of yellow = 70

number of counters of red = 30

a) Fractional part of red counters = 30/100

After the simplification, we get 3/10

b) Fractional part of yellow counters = 70/100

After the simplification, we get 7/10

c) Converting number of red counters as percentage

30/100 = 30%

d) Converting number of yellow counters as percentage 

70/100 = 70%

e) Percentage of yellow counters is greater than percentage of red counters.

What fraction, decimal and prercentage of each grid is shaded blue ?

Example 5 :

Solution :

1 grid is shaded out of 100 grids.

• Fraction = 1/100
• Decimal = 0.01
• Percentage = 1%

Example 6 :

Fill in the missing numbers.

a)  9/10 = ___ / 100 = ____ %

b)  9/50 = ___ / 100 = _____ %

c)  9/20 = ___ / 100 = _____ %

d) 9/25 = ___ / 100 = _____ %

Solution :

a)  9/10 =

To make the denominator as 100, we multiply both numerator and denominator by 10.

= (9/10) x (10/10)

= 90/100

= 90%

b)  9/50 =

To make the denominator as 100, we multiply both numerator and denominator by 2.

= (9/50) x (2/2)

= 18/100

= 18%

c)  9/20 =

To make the denominator as 100, we multiply both numerator and denominator by 5.

= (9/20) x (5/5)

= 45/100

= 45%

d) 9/25 =

To make the denominator as 100, we multiply both numerator and denominator by 4.

= (9/25) x (4/4)

= 36/100

= 36%

Example 7 :

Shade the grid in the given proportions.

a)  3/5 green

b) 14% red

c)  4/20 blue 

d) the rest yellow

e) What percentage of grid is yellow ?

Solution :

a)  3/5 green

To conver the denominator as 100, we multiply by 20

= (3/5) x (20/20)

= 60/100

So, we have to shade 60 grids out of grids using the coulour green.

b) 14% red

Converting 14% as fraction, we get

= 14/100

Out of 100 grids, shade 14 grids with the colour of red.

c)  4/20 blue 

Converting the denominator as 100, we have to multiply both numerator and denominator by 5, we get

= (4/20) x (5/5)

= 20/100

Out of 100 grids, we have to shade 20 grids with the colour of blue.

d) the rest yellow

e) 100/100 - 20/100

= 80/100

So, percentage of yellow grids is 80%.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.