MISSING SIDE OF A RIGHT TRIANGLE WORKSHEET

1. In the right triangle shown below, find the value of 'a'.

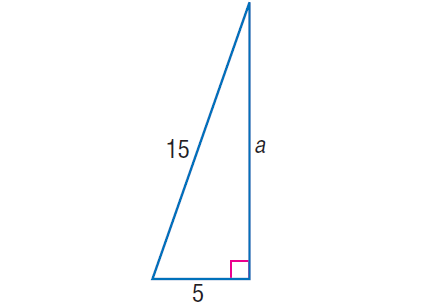
2. In the right triangle shown below, find the value of 'c'.

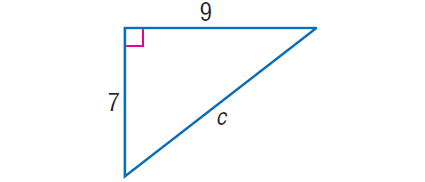
3. In the right triangle shown below, find the value of 'c'.

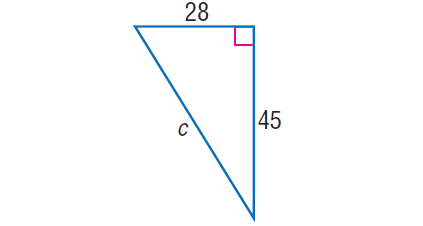
4. In the right triangle shown below, find the value of 'b'.

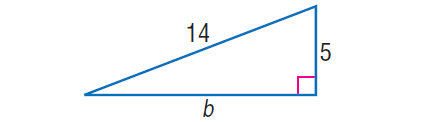
5. In the right triangle shown below, find the value of 'a'.

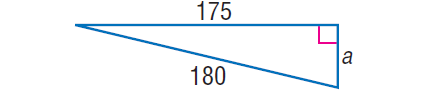
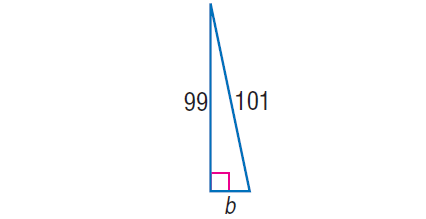
6. In the right triangle shown below, find the value of 'b'.

7. Let a, b and c be the lengths of the sides of a right triangle. If a = 16, b = 63 and c is the length of hypotenuse, then find the value of c.

8. Let a, b and c be the lengths of the sides of a right triangle. If a = 16, c = 34 and c is the length of hypotenuse, then find the value of b.

9. Let a, b and c be the lengths of the sides of a right triangle. If b = √112, c = 3 and a is the length of hypotenuse, then find the value of a.

10. Let a, b and c be the lengths of the sides of a right triangle. If a = 7y, c = 3y and a is the length of hypotenuse, then find the value of b in terms of y.

1. Answer :

In the right triangle above, by Pythagorean Theorem,

15²  =  5² + a² 

225  =  25 + a² 

Subtract 25 from both sides.

200 = a²

Take square root on both sides.

√200 = √a²

√(2 x 10 x 10) = a

10√2 = a

2. Answer :

In the right triangle above, by Pythagorean Theorem,

c² = 7² + 9²

c² = 49 + 81

c² = 130

Take square root on both sides.

√c² = √130

c = √130

3. Answer :

In the right triangle above, by Pythagorean Theorem,

c² = 28² + 45²

c² = 784 + 2025

c² = 2809

Take square root on both sides.

√c = √2809

c = 53

4. Answer :

In the right triangle above, by Pythagorean Theorem,

14² = 5² + b²

196 = 25 + b²

Subtract 25 from both sides.

171 = b²

√171 = √b²

√171 = b

5. Answer :

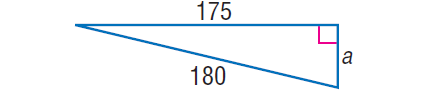
In the right triangle above, by Pythagorean Theorem,

180² = a² + 175²

32400 = a² + 30625

Subtract 30625 from both sides.

1775 = a²

√1775 = √a²

√(5 x 5 x 71) = a

5√71 = a

6. Answer :

In the right triangle above, by Pythagorean Theorem,

101² = b² + 99²

10201 = b² + 9801

Subtract 9801 from both sides.

400 = b²

√400 = √b²

20 = b

7. Answer :

By Pythagorean Theorem,

c² = a² + b²

Substitute a = 16 and b = 63.

c² = 16² + 63²

c² = 256 + 3969

c² = 4225

Take square root on both sides.

√c² = √4225

c = 65

8. Answer :

By Pythagorean Theorem,

c² = a² + b²

Substitute a = 16 and c = 34.

34² = 16² + b²

1156 = 256 + b²

Subtract 256 from both sides.

900 = b²

Take square root on both sides.

√900 = √b²

30 = b

9. Answer :

By Pythagorean Theorem,

a² = b² + c²

Substitute b = √112 and c = 3.

a² = (√112)² + 3²

a² = 112 + 9

a² = 121

Take square root on both sides.

√a² = √121

a = 11

10. Answer :

a² = b² + c²

(7y)² = b² + (3y)²

49y² = b² + 9y²

Subtract 9y² from both sides.

40y² = a²

Take square root on both sides.

√(40y²) = √a²

2y√10 = a

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.