THE MIDPOINT AND DISTANCE FORMULAS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
The midpoint of a line segment is the point that divides the segment into two congruent segments. Congruent segments are segments that have the same length.
You can find the midpoint of a segment by using the coordinates of its endpoints. Calculate the average of the x-coordinates and the average of the y-coordinates of the endpoints.
Midpoint Formula
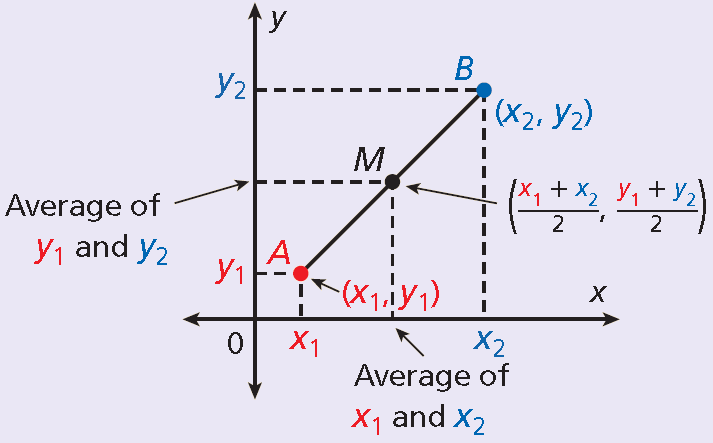
Let A(x1, y1) and B(x2, y2).
The midpoint M of the line segment AB is
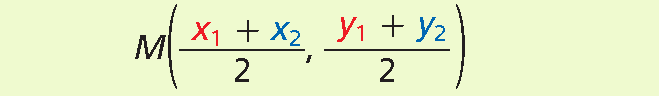
Finding the Coordinates of a Midpoint
Example 1 :
Find the coordinates of the midpoint of the line segment CD with endpoints C(-2, -1) and D (4, 2).
Solution :
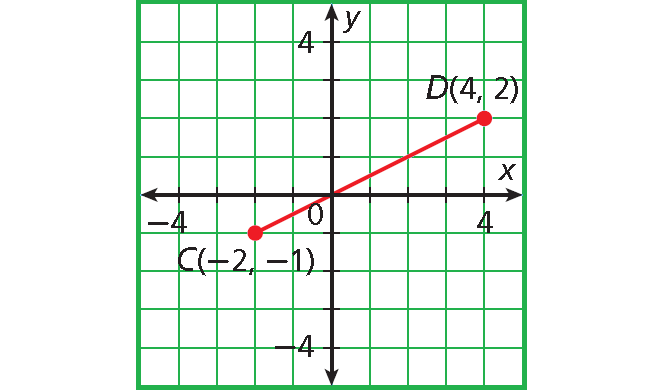
Write the formula.
Substitute (-2, -1) for (x1, y1) and (4, 2) for (x2, y2).
= M[⁽⁻² ⁺ ⁴⁾⁄₂, ⁽⁻¹ ⁺ ²⁾⁄₂]
= M(²⁄₂, ½)
= M(1, ½)
Finding the Coordinates of an Endpoint
Example 2 :
M is the midpoint of the line segment AB. A has coordinates (2, 2), and M has coordinates (4, -3). Find the coordinates of B.
Solution :
Step 1 :
Let the coordinates of B equal (x, y).
Step 2 :
Use the Midpoint Formula.
(4, -3) = [⁽² ⁺ ˣ⁾⁄₂, ⁽² ⁺ ʸ⁾⁄₂]
Step 2 :
|
Find the x-coordinate. 4 = ⁽² ⁺ ˣ⁾⁄₂ 8 = 2 + x 6 = x |
Find the y-coordinate. -3 = ⁽² ⁺ ʸ⁾⁄₂ -6 = 2 + y -8 = y |
The coordinates of B are (6, –8).
Check :
Graph points A and B and midpoint M.
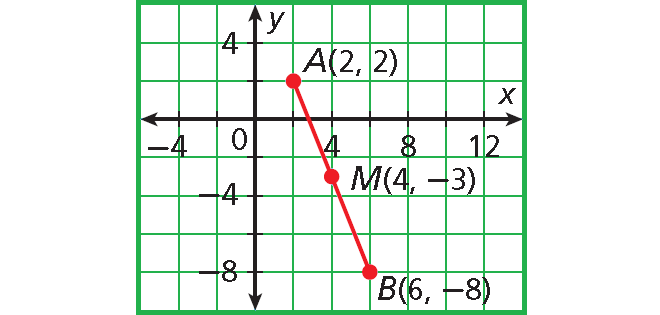
Point M appears to be the midpoint of the line segment AB.
You can also use coordinates to find the distance between two points or the length of a line segment.
To find the length of segment PQ, draw a horizontal segment from P and a vertical segment from Q to form a right triangle as shown below.
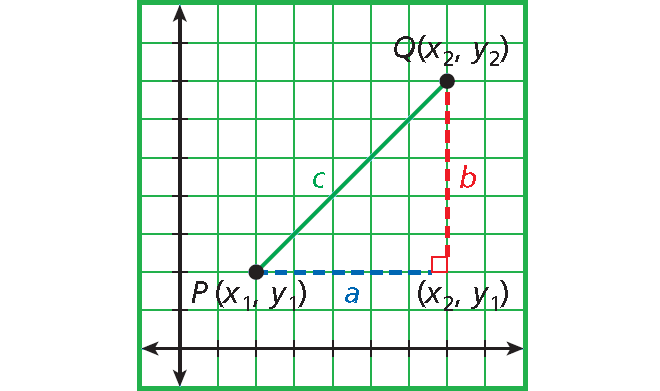
Pythagorean Theorem :
c2 = a2 + b2
Solve for c. Use the positive square root to represent distance.
c = √(a2 + b2)
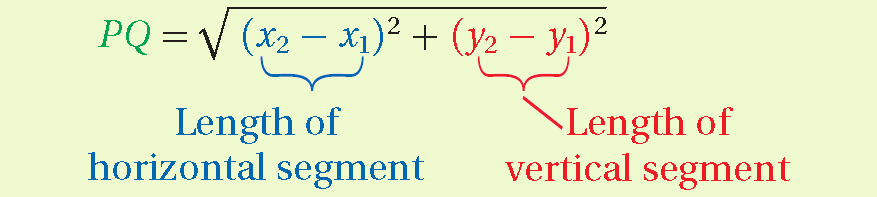
This equation represents the Distance Formula.
Distance Formula
In a coordinate plane, formula to find the distance between two points (x1, y1) and (x2, y2) is
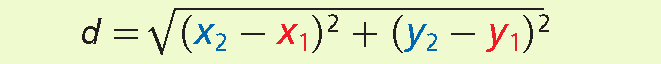
Finding Distance in the Coordinate Plane
Example 3 :
Use the Distance Formula to find the distance, to the nearest hundredth, from A(-2, 3) to B(2, -2).
Solution :
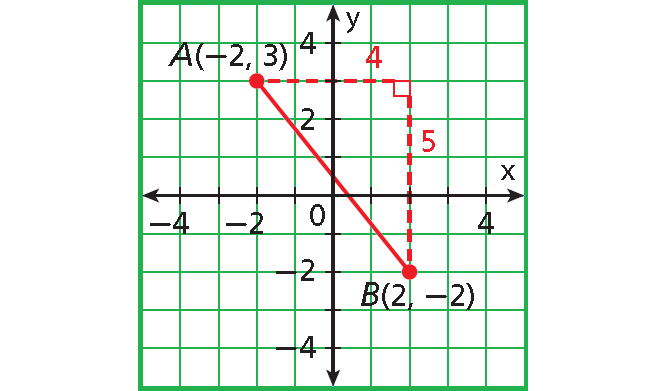
Distance Formula :
d = √[(x2 - x1)2 + (y2 - y1)2]
Substitute (-2, 3) for (x1, y1) and (2, -2) for (x2, y2).
d = √[(2 + 2)2 + (-2 - 3)2]
Simplify.
d = √[42 + (-5)2]
d = √[16 + 25]
d = √41
d ≈ 6.40
The distance between from A(-2, 3) to B(2, -2) is about 6.40 units.
Geography Application
Example 4 :
Each unit on the map of Lake Okeechobee represents 1 mile. Kemka and her father plan to travel from point A near the town of Okeechobee to point B at Pahokee. To the nearest tenth of a mile, how far do Kemka and her father plan to travel?
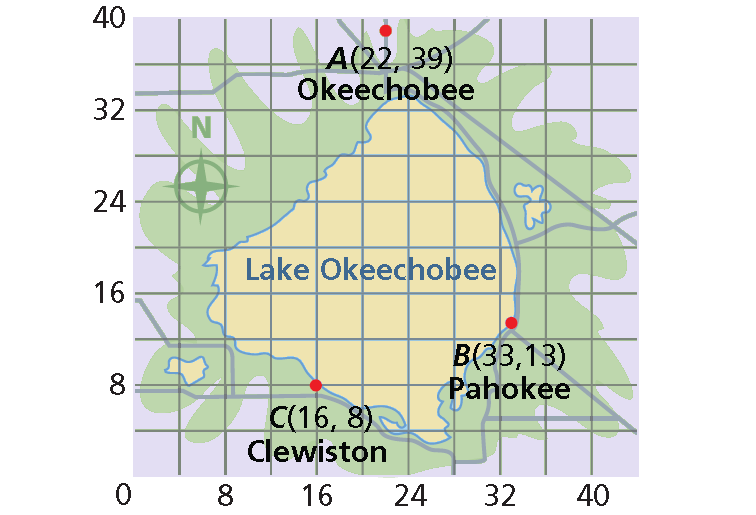
Solution :
Distance Formula :
d = √[(x2 - x1)2 + (y2 - y1)2]
Substitute (33, 13) for (x1, y1) and (22, 39) for (x2, y2).
d = √[(33 - 22)2 + (13 - 39)2]
Simplify.
d = √[112 + (-26)2]
d = √[121 + 676]
d = √797
d ≈ 28.2
Kemka and her father plan to travel about 28.2 miles.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 50)
Mar 06, 26 07:48 PM
Digital SAT Math Problems and Solutions (Part - 50) -
Digital SAT Math Problems and Solutions (Part - 49)
Mar 06, 26 06:47 PM
Digital SAT Math Problems and Solutions (Part - 49) -
Digital SAT Math Problems and Solutions (Part - 48)
Mar 06, 26 05:24 PM
Digital SAT Math Problems and Solutions (Part - 48)


