USING THE MIDPOINT FORMULA WORKSHEET

1. The mid points of the sides of a triangle are (2, 4), (-2, 3) and (5, 2). Find the coordinates of the vertices of the triangle.

2. O(0, 0) is the center of a circle whose one chord is AB, where the points A and B are (8, 6) and (10, 0) respectively. If OD is the perpendicular from the center to the chord AB, find the coordinates of the mid point of OD.

3. The points A(-5, 4), B(-1, -2) and C(5, 2) are the vertices of an isosceles right angled triangle where the right angle is at B. Find the coordinates of D so that ABCD is a square.

4.  PQRS is a rectangle formed by joining the points P(-1, -1), Q(-1, 4), R(5, 4) and S(5, -1). A, B, C and D are the mid-points of PQ, QR, RS and SP respectively. Is the quadrilateral ABCD a square, a rectangle or a rhombus? Justify your answer.

1. Answer :

Let D, E and F be the mid points of the sides AB, BC and CA of ΔABC.

D(x₁, y₁) = (2, 4)

E(x₂, y₂) = (-2, 3)

F(x₃, y₃) = (5, 2)

The vertices of ΔABC can be found as shown below.

A(x₁ + x₃ - x_2, y₁ + y₃ - y₂)

B(x₁ + x₂ - x_3, y₁ + y₂ - y₃)

C(x₂ + x₃ - x_1, y₂ + y₃ - y₁)

Vertex A :

A(x₁ + x₃ - x_2, y₁ + y₃ - y₂)

A(2 + 5 + 2, 4 + 2 - 3)

A(9, 3)

Vertex B :

B(x₁ + x₂ - x_3, y₁ + y₂ - y₃)

B(2 - 2 - 5, 4 + 3 - 2)

B(-5, 5)

Vertex C :

C(x₂ + x₃ - x_1, y₂ + y₃ - y₁)

C(-2 + 5 - 2, 3 + 2 - 4)

C(1, 1)

2. Answer :

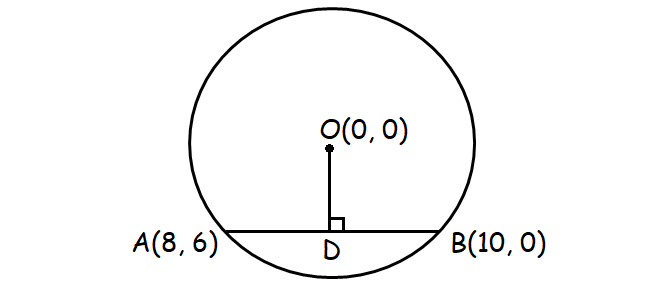
The perpendicular drawn from the center of a circle to a chord will always intersect at the mid point of the chord.

Since OD is the perpendicular from the center to the chord AB, D is the mid point of the chord AB. 

Point D : 

Formula to find the mid point :

= ((x₁ + x₂)/2, (y₁ + y₂)/2)

Substitute (x₁, y₁) = A(8, 6) and (x₂, y₂) = B(10, 0).

= ((8 + 10)/2, (6 + 0)/2)

= (18/2, 6/2)

= D(9, 3)

Mid point of OD :

= ((x₁ + x₂)/2, (y₁ + y₂)/2)

Substitute (x₁, y₁) = O(0, 0) and (x₂, y₂) = D(9, 3).

= ((0 + 9)/2, (3 + 0)/2)

= (9/2, 3/2)

3. Answer :

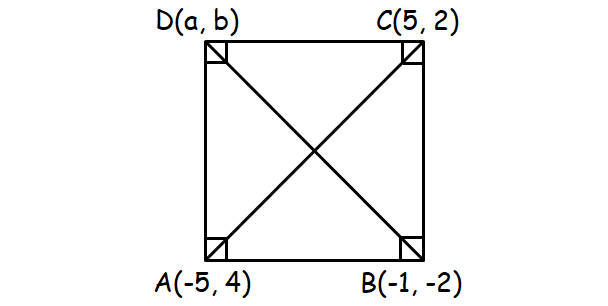
Mid point of AC :

= ((x₁ + x₂)/2, (y₁ + y₂)/2)

Substitute (x₁, y₁) = A(-5, 4) and (x₂, y₂) = C(5, 2).

= ((-5 + 5)/2, (4 + 2)/2)

= (0, 6/2)

= (0, 3)

Mid point of BD :

= ((x₁ + x₂)/2, (y₁ + y₂)/2)

Substitute (x₁, y₁) = B(-1, -2) and (x₂, y₂) = D(a, b).

= ((-1 + a)/2, (-2 + b)/2)

Since ABCD is a square, the diagonals AC and BD will bisect each other. Mid point of AC and mid point of BD are equal. 

((-1 + a)/2, (-2 + b)/2) = (0, 3)

If two points are equal, then the x coordinates and y coordinates must be equal. 

The coordinates of D : (1, 8).

4. Answer :

• Midpoint of side PQ = A
• Midpoint of side QR = B
• Midpoint of side RS = C
• Midpoint of side SP = D

Midpoint = ((x₁ + x₂)/2, (y₁ + y₂)/2)

Midpoint of PQ :

P(-1, -1) and Q(-1, 4)

A = (-1 - 1)/2, (-1 + 4)/2

= -2/2, 3/2

A = (-1, 3/2)

Midpoint of QR :

Q(-1, 4) and R(5, 4)

B = (-1 + 5)/2, (4 + 4)/2

= 4/2, 8/2

B = (2, 4)

Midpoint of RS :

R(5, 4) and S(5, -1)

C = (5 + 5)/2, (4 - 1)/2

= 10/2, 3/2

C = (5, 3/2)

Midpoint of SP :

S(5, -1) and P(-1, -1)

D = (5 - 1)/2, (-1 - 1)/2

= 4/2, -2/2

D = (2, -1)

A (-1, 3/2), B (2, 4), C (5, 3/2) and D (2, -1)

Distance between AB = √[(x₂ - x₁)² + (y₂ - y₁)²]

= √[(2 + 1)² + (4 - 3/2)²]

= √[3² + (5/2)²]

= √9 + (25/4)

= √61/2

Distance between BC = √[(5 - 2)² + (3/2 - 4)²]

= √[3² + (-5/2)²]

= √9 + (25/4)

= √61/2

Distance between CD = √[(2 - 5)² + (-1 - 3/2)²]

= √[3² + (-5/2)²]

= √9 + (25/4)

= √61/2

Distance between DA = √[(2 + 1)² + (-1-3/2)²]

= √[3² + (-5/2)²]

= √9 + (25/4)

= √61/2

Since all sides are equal, it may be a square or rhombus.

To prove rhombus, we have to prove angle measure at vertex is 90 degree.

Slope of AB = (y₂ - y₁)/(x₂ - x₁)

A (-1, 3/2), B (2, 4)

= (4 - 3/2) / (2 + 1)

= 5/2 / 3

= 5/6

Slope of BC = (y₂ - y₁)/(x₂ - x₁)

B (2, 4), C (5, 3/2)

= (3/2 - 4) / (5 - 2)

= -5/2 / 3

= -5/6

The product of their slopes is not equal to -1, then it is rhombus not a square.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.