MEDIANS AND ALTITUDES OF A TRIANGLE

Median of a Triangle

A median of a triangle is a segment whose endpoints are a vertex of the triangle and the midpoint of the opposite side. For instance, in ΔABC shown below, D is the midpoint of side BC. So, AD is the median of the triangle ABC.

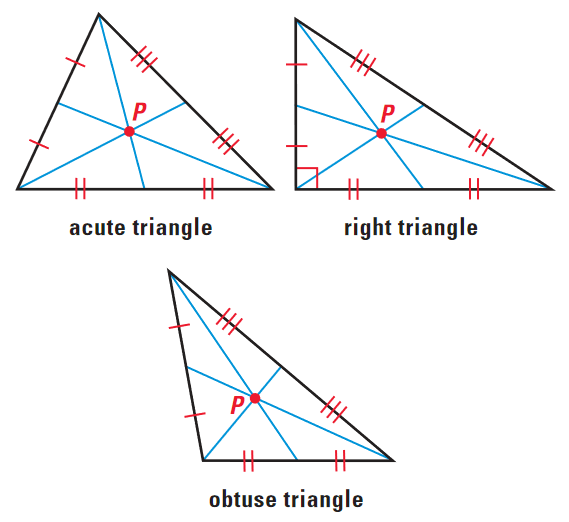
The three medians of a triangle are concurrent. The point of concurrency is called the centroid of the triangle. The centroid, labeled P in the diagrams below, is always inside the triangle.

Altitude of a Triangle

An altitude of a triangle is the perpendicular segment from a vertex to the opposite side or to the line that contains the opposite side. An altitude can lie inside, on, or outside the triangle.

Every triangle has three altitudes. The lines containing the altitudes are concurrent and intersect at a point called the orthocenter of the triangle.

Concurrency of Altitudes of a Triangle

The medians of a triangle intersect at a point that is two thirds of the distance from each vertex to the midpoint of the opposite side.

If P is the centroid of ΔABC, then

AP = (2/3)AD

BP = (2/3)BF

CP = (2/3)CE 

Concurrency of Medians of a Triangle

The lines containing the altitudes of a triangle are concurrent.

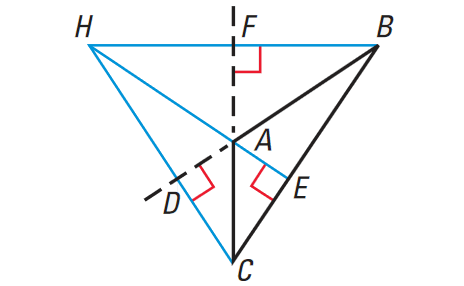
If AE, BF and CD are the altitudes of ΔABC, then the lines AE, BF and CD intersect at some point H.

Solved Examples

Example 1 :

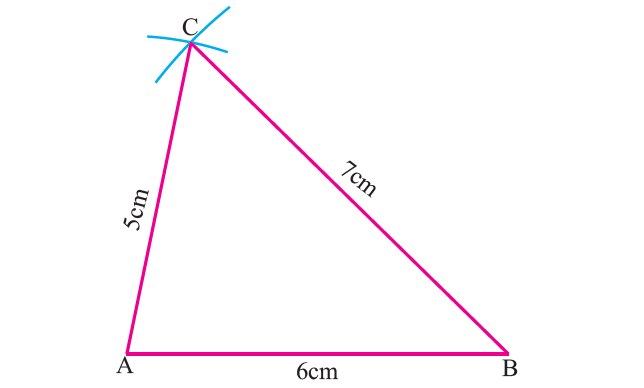
Construct the centroid of ΔABC whose sides are AB = 6cm, BC = 7cm, and AC = 5cm.

Solution :

Step 1 :

Draw ΔABC using the given measurements.

Step 2 :

Construct the perpendicular bisectors of any two sides (AC and BC) to find the mid points D and E of AC and BC respectively.

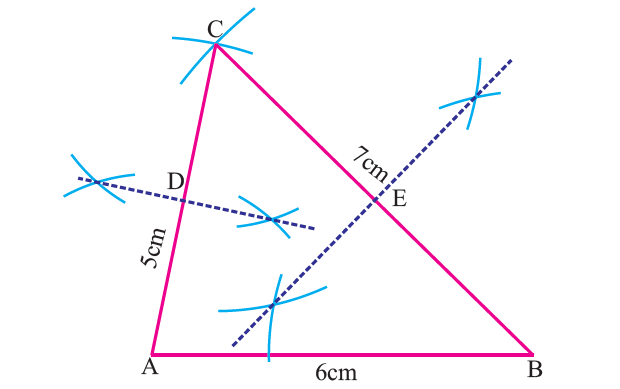
Step 3 :

Draw the medians AE and BD and let them meet at G.

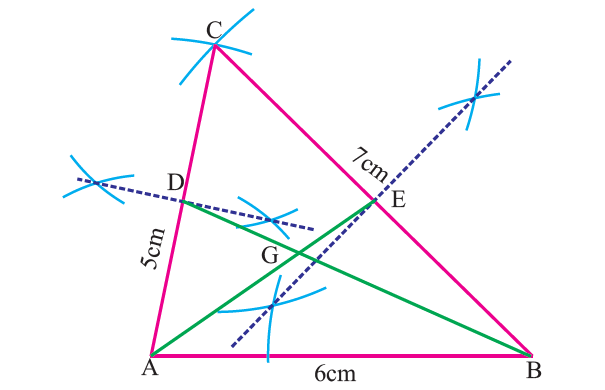
The point G is the centroid of the given ΔABC.

Example 2 :

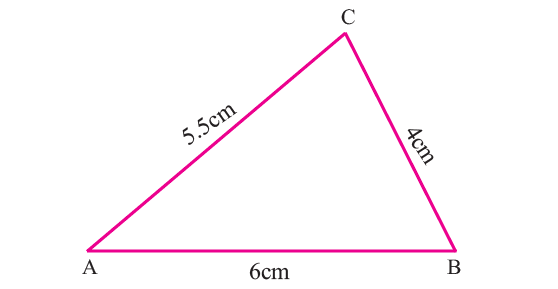
Construct ΔABC whose sides are AB = 6cm, BC = 4cm and AC = 5.5cm and locate its orthocenter.

Solution :

Step 1 :

Draw ΔABC using the given measurements.

Step 2 :

Construct altitudes from any two vertices (A and C) to their opposite sides (BC and AB respectively).

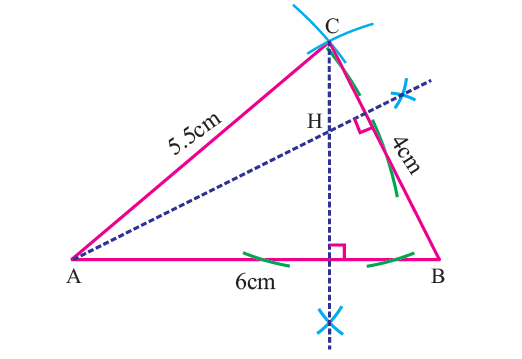
The point of intersection of the altitudes H is the orthocenter of the given ΔABC.

Example 3 :

Where is the orthocenter located in each type of triangle ?

(a) Acute triangle

(b) Right triangle

(c) Obtuse triangle

Solution :

Draw an example of each type of triangle and locate its orthocenter.

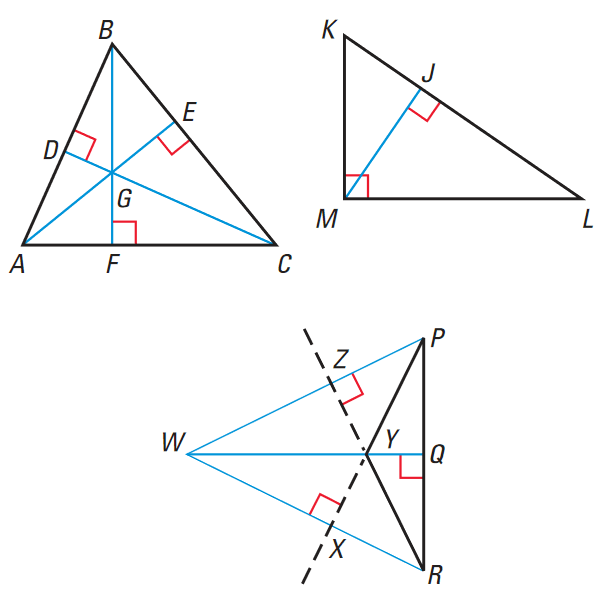
(a) Acute Triangle :

ΔABC is an acute triangle. The three altitudes intersect at G, a point inside the triangle.

(a) Right Triangle :

ΔKLM is a right triangle. The two legs LM and KM, are also altitudes. They intersect at the triangle's right angle. This implies that the orthocenter is on the triangle at M, the vertex of the right angle of the triangle.

(a) Obtuse Triangle :

ΔYPR is an obtuse triangle. The three lines that contain the altitudes intersect at W, a point that is outside the triangle.

Example 4 :

Find the coordinates of the centroid of ΔJKL shown below.

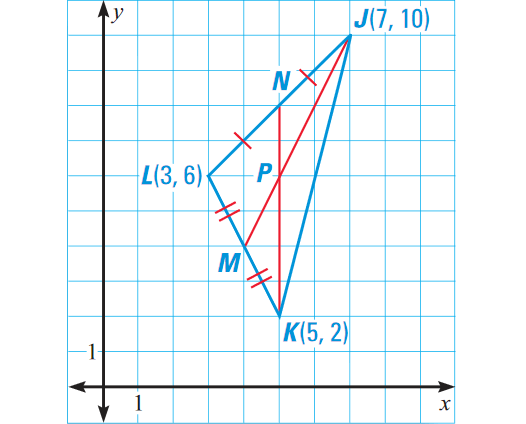
Solution :

We know that the centroid is two thirds of the distance from each vertex to the midpoint of the opposite side.

Choose the median KN. Find the coordinates of N, the midpoint of JL.

The coordinates of N are

[(3 + 7)/2, (6 + 10)/2] = (10/2, 16/2)

= (5, 8)

Find the distance from vertex K to midpoint N. The distance from K(5, 2) to N(5, 8) is 8 - 2, or 6 units.

Determine the coordinates of the centroid, which is 2/3⋅6 or 4 units up from vertex K along the median KN.

Hence, the coordinates of centroid P are

(5, 2 + 4) or (5, 6)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.