MEAN MEDIAN AND MODE WORKSHEET

Question 1 :

Find the mean, median and  mode of the data set.

{132, 149, 152, 164, 164, 175}

Question 2 :

In a geometry class of 15 boys and 12 girls, the average (arithmetic mean) test score of the class was 81. If the average score of the 15 boys was 83, what was the average score of the 12 girls?

Question 3 :

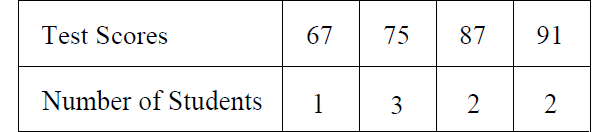
The test scores of 8 students are shown in the table above. Let m be the mean of the scores and M be the median of the score. What is the value of M - m?

A) -6

B) 0

C) 3

D) 6

Question 4 :

n, n - 3, 2n - 1, 3n - 4 and 5n + 12

The average (arithmetic mean) of five numbers given above is 8. Which of of the following is true?

A) median = 5, mode = 7

B) median = 5, mode = 5

C) median = 7, mode = 7

D) median = 7, mode = 5

Question 5 :

The average (arithmetic mean) of two numbers is

(1/2)x + 1

If one of the numbers is x, what is the other number?

A) 2 + x

B) 2 - x

C) -2

D) 2

Question 6 :

The average (arithmetic mean) of a set of n numbers is 19. If the average of the 6 greatest numbers in the set is 29 and the average of the remaining numbers is 7, what is the value of n?

A) 9

B) 10

C) 11

D) 12

Question 7 :

The average (arithmetic mean) of m, n, and -1 is 0. What is the value of m + n?

Question 8 :

A student has an average (arithmetic mean) score of 86 points for 4 tests. What total score does this student need in the next two tests in order to have an average of 90 for all 6 tests?

1. Answer :

Mean :

= sum of the values/number of values

= (132 + 149 + 152 + 164 + 164 + 175)/6

= 936/6

= 156

Median :

132, 149, 152, 164, 164, 175

The values in the data given are already arranged from least to greatest.

Formula to find median :

= [(n + 1)/2]^th value

Substitute n = 6.

= [(6 + 1)/2]^th value

= (7/2)^th value

= 3.5^th value

= average of 3^rd and 4^th values

= (152 + 164)/2

Mode :

In the data given {132, 149, 152, 164, 164, 175}, the value 164 appears more number of times, that is twice.

So, mode = 164.

2. Answer :

Let

x̄ ---> average test score of the class, x̄ = 81

x̄₁ ---> average test score of 15 boys, x̄₁ = 83

x̄₂ ---> average test score of 15 girls, x̄₂ = ?

n₁ ---> number of boys, n₁ = 15

n₂ ---> number of girls, n₂ = 12

Combined Mean :

Substitute x̄ = 81, x̄₁ = 83, n₁ = 15 and n₂ = 12.

The average score of 12 girls is 78.5.

3. Answer :

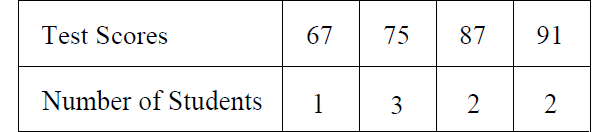
Find the mean :

Sum of the scores :

= 1x67 + 3x75 + 2x87 + 2x91

= 67 + 225 + 174 + 182

= 648

Total number of students :

= 1 + 3 + 2 + 2

= 8

Mean :

m = 648/8

m = 81

Find the median :

Given data :

67, 75, 75, 75, 87, 87, 91, 91

The values in the given data are already arranged from least to greatest.

Formula to find median :

= [(n + 1)/2]^th value

Substitute n = 8.

= [(8 + 1)/2]^th value

= (9/2)^th value

= 4.5^th value

= average of 4^th and 5^th values

= (75 + 87)/2

= 81

median, M = 81

M - m = 81 - 81

M - m = 0

The correct answer choice is (B).

4. Answer :

Average of five numbers = 8

(n + n - 3 + 2n - 1 + 3n - 4 + 5n + 12)/5 = 8

(12n + 4)/5 = 8

Multiply both sides by 5.

12n + 4 = 40

Subtract 4 from both sides.

12n = 36

Divide both sides by 12.

n = 3

Then,

n - 3 = 0

2n - 1 = 5

3n - 4 = 5

5n + 12 = 27

The given five numbers are 3, 0, 5, 5 and 27.

Arrange the numbers from least to greatest.

0, 3, 5, 5, 27

median = 5

mode = 5

The correct answer choice is (B).

5. Answer :

Let y be the other number.

Average of x and y is (1/2)x + 1.

(x + y)/2 = (1/2)x + 1

(x + y)/2 = (x/2) + 1

(x + y)/2 = (x + 2)/2

Multiply both sides by 2.

x + y = x + 2

Subtract x from both sides.

y = 2

The other number is 2.

The correct answer choice is (D).

6. Answer :

Average of the 6 greatest numbers = 29

Sum of the 6 greatest numbers/6 = 29

Sum of the 6 greatest numbers = 174

Number of remaining numbers = n - 6.

Average of the remaining (n - 6) numbers = 7

[Sum of the remaining (n - 60) numbers]/(n - 6) = 7

Sum of the remaining (n - 60) numbers = 7(n -6)

Sum of all n numbers = 174 + 7(n - 6)

= 174 + 7n - 42

= 7n + 132

Average of a set of n numbers = 19

Sum of n numbers/n = 19

(7n + 132)/n = 19

7n + 132 = 19n

132 = 12n

11 = n

The correct answer choice is (C).

7. Answer :

Average of m, n, and -1 = 0

(m + n - 1)/3 = 0

Multiply both sides by 3.

m + n - 1 = 0

Add 1 to both sides.

m + n = 1

8. Answer :

Average of scores in 4 tests = 86

Sum of scores in 4 tests/4 = 86

Multiply both sides by 4.

Sum of scores in 4 tests = 344

Let x be the total score in the next two tests.

Average of scores in 6 tests = 90

(Sum of scores in 4 tests + x)/6 = 90

(344 + x)/6 = 90

Multiply both sides by 6.

344 + x = 540

Subtract 344 from both sides.

x = 196

So the total score needed on the next two tests is 196.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.