MEAN DEVIATION

Since range is based on only two observations, it is not regarded as an ideal measure of dispersion. 

A better measure of dispersion is provided by mean- deviation which, unlike range, is based on all the observations.

For a given set of observation, mean-deviation is defined as the arithmetic mean of the absolute deviations of the observations from an appropriate measure of central tendency.

Let the  variable 'x' assume 'n' values  as given below

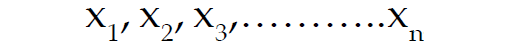
Then the mean-deviation of x about an average A is given by

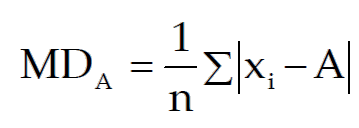
For a grouped frequency distribution, mean-deviation about A is given by

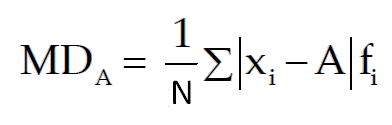
Where, N  =  ∑f

In most cases we take A as mean or median and accordingly, we get mean-deviation about mean or mean deviation about median.

Coefficient of Mean Deviation

A relative measure of dispersion applying mean-deviation is given by

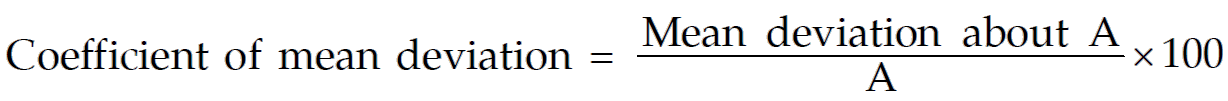
Mean-deviation takes its minimum value when the deviations are taken from the median.

Also mean-deviation remains unchanged due to a change of origin but changes in the same ratio due to a change in scale

i.e. if y = a + bx, a and b being constants,

then MD of y = |b| × MD of x

Properties of Mean Deviation

1)  Mean-deviation takes its minimum value when the deviations are taken from the median.

2)  Mean-deviation remains unchanged due to a change of origin but changes in the same ratio due to a change in scale

i.e. if y = a + bx, a and b being constants,

then MD of y = |b| × MD of x

3)  It is rigidly defined

4) It is based on all the observations and not much affected by sampling fluctuations.

5)  It is difficult to comprehend and its computation

6) Furthermore, unlike SD, mean-deviation does not possess mathematical properties.

Solved Problems

Problem 1 : 

What is the mean-deviation about mean for the following numbers?

5, 8, 10, 10, 12, 9

Solution :

The mean is given by

x̄  =  (5 + 8 + 10 + 10 + 12 + 9) / 6

x̄  =   54 / 6

x̄  =   9

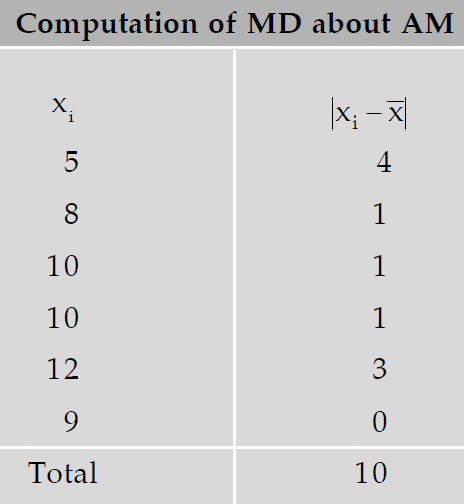
Thus mean-deviation about mean is given by

∑|x - x̄ | / n  =  10 / 6  =  1.67

So, mean-deviation for the given data is 1.67

Problem 2 : 

Find mean-deviation about median and also the corresponding coefficient for the following observations. 

82, 56, 75, 70, 52, 80, 68

Solution :

The given observations are in ascending order.

Number of observations  =  7

Median  =  (n + 1)/2  th value 

Median  =  (7+1)/2  th value   

Median  =  8/2  th value 

Median  =  4^th value 

Median  =  70

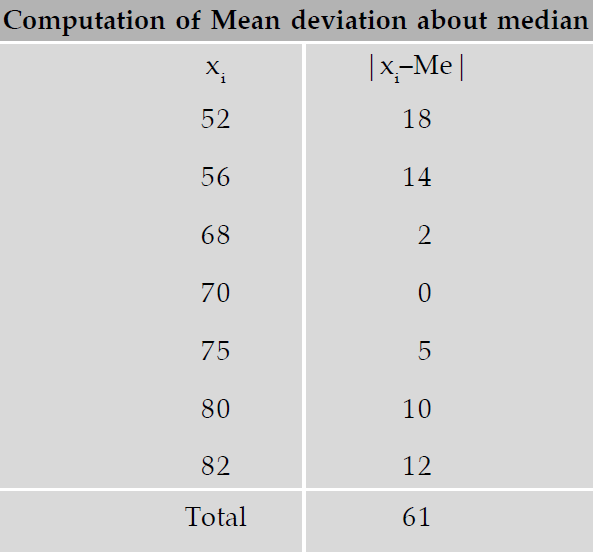
Thus mean-deviation about median is given by

∑|x - median| / n  =  61 / 7  =  8.71

So, mean-deviation for the given data is 8.71.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.