MEAN AS A BALANCE POINT
Mean can be defined as a balance point on a number line where
the data distribution is balanced.
This means that the sum of the distances from the mean of all the points above the mean is equal to the sum of the distances of all the data points below the mean.
In more detail :
Th quantity on each side of mean (balance point) on a number line will be equal.
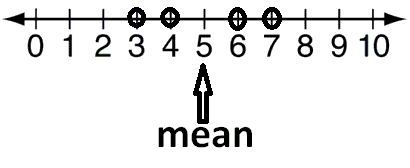
Example 1 :
Where is the balance point for this data ?
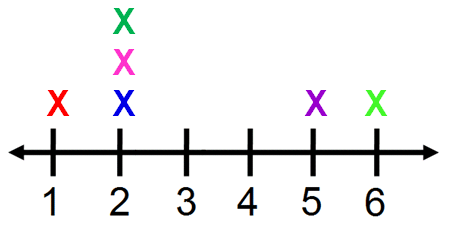
Solution :
Example 2 :
Where is the balance point for this data ?
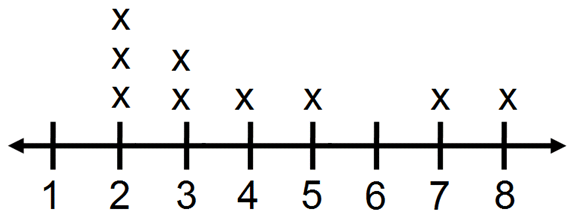
Solution :
Example 3 :
Where is the balance point for this data ?
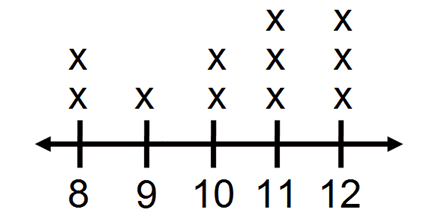
Solution :
Solved Problems
Problem 1 :
A set of data has four values. Three of the values are plotted on the number line below.
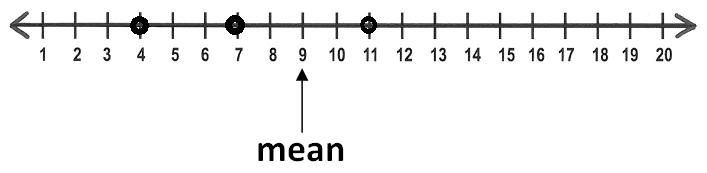
Where should the fourth point be plotted so the mean of the data set is 9 ?
Solution :
Step 1 :
Let us consider on the left side of the mean 9. Two points are marked on the number line. They are 7 and 4.
7 is two spaces away from the mean and 4 is five spaces away from the mean.
Total on the left side is
= 2 spaces + 5 spaces
= 7 spaces
Step 2 :
On the right side also we should have the same no. of spaces if the mean is 9.
Already there is a point on the right side of the mean, that is 11. And 11 is two spaces away from the mean.
So we need five more spaces on the right side in order to have the total of seven spaces.
Step 3 :
Now, Just pick a point on the right side which is five spaces away from the mean 9. That is 14.
Therefore, the fourth point should be plotted at 14.
Problem 2 :
A set of data has four values. Three of the values are plotted on the number line below.
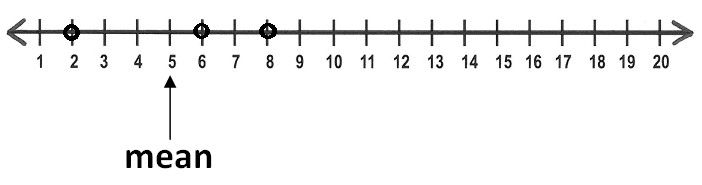
Where should the fourth point be plotted so the mean of the data set is 5 ?
Solution :
Step 1 :
Let us consider on the right side of the mean 5. Two points are marked on the number line. They are 6 and 8.
6 is one space away from the mean and 8 is three spaces away from the mean.
Total on the right side is
= 1 space + 3 spaces
= 4 spaces
Step 2 :
On the left side also we should have the same number of spaces, if the mean is 5.
Already there is a point on the left side of the mean, that is 2. And 2 is three spaces away from the mean.
So we need one more space on the left side in order to have the total of four spaces.
Step 3 :
Now, Just pick a point on the left side which is one space away from the mean 5. That is 4.
Therefore, the fourth point should be plotted at 4.
Problem 3 :
A set of data has 3 values. Two of the values are plotted on the number line below.
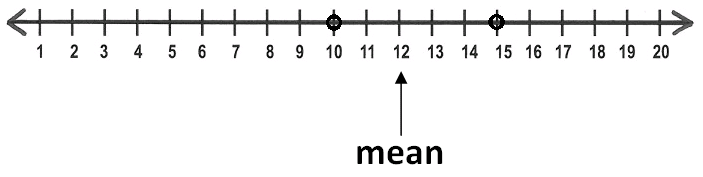
Where should the third point be plotted so the mean of the data set is 12 ?
Solution :
Step 1 :
Let us consider on the right side of the mean 12. Only one point is marked and it is 15.
15 is three spaces away from the mean.
Total on the right side is three spaces.
Step 2 :
On the left side also we should have the same number of spaces, if the mean is 12.
Already there is a point on the left side of the mean, that is 10. And 10 is two spaces away from the mean.
So we need one more space on the left side in order to have the total of three spaces.
Step 3 :
Now, Just pick a point on the left side which is one space away from the mean 12. That is 11.
Therefore, the fourth point should be plotted at 11.
Problem 4 :
A set of data has 4 values. Three of the values are plotted on the number line below
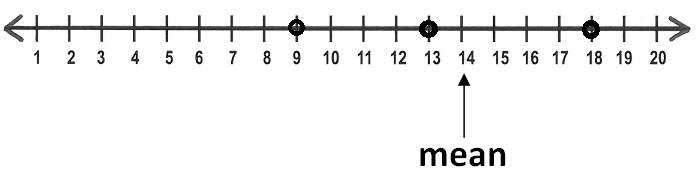
Where should the fourth point be plotted so the mean of the data set is 14 ?
Solution :
Step 1 :
Let us consider on the left side of the mean 14. Two points are marked on the number line. They are 9 and 13.
9 is five spaces away from the mean and 13 is one space away from the mean.
Total on the left side is
= 5 spaces + 1 space
= 6 spaces
Step 2 :
On the right side also we should have the same number of spaces, if the mean is 14.
Already there is a point on the right side of the mean, that is 18. And 18 is four spaces away from the mean.
So we need two more spaces on the right side in order to have the total of six spaces.
Step 3 :
Now, Just pick a point on the right side which is two spaces away from the mean 14. That is 16.
Therefore, the fourth point should be plotted at 16.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
WORD PROBLEMS
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Markup and markdown word problems
Word problems on mixed fractions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Word problems on sets and Venn diagrams
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Time, speed and distance shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the word problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by 7
Sum of all three digit numbers divisible by 8
Sum of all three digit numbers formed using 1, 3, 4
Sum of all three four digit numbers formed with non zero digits
Sum of all three four digit numbers formed using 0, 1, 2, 3
Sum of all three four digit numbers formed using 1, 2, 5, 6
©All rights reserved. onlinemath4all.com
Recent Articles
-
Linear Growth and Decay
May 22, 22 03:05 AM
Linear Growth and Decay
-
Worksheet on Probability
May 22, 22 01:15 AM
Worksheet on Probability
-
Probability Worksheet
May 22, 22 01:12 AM
Probability Worksheet