MATHEMATICAL INDUCTION EXAMPLES

About "Mathematical Induction Examples"

Mathematical Induction Examples :

Here we are going to see some mathematical induction problems with solutions.

Define mathematical induction :

Mathematical Induction is a method or technique of proving mathematical results or theorems

The process of induction involves the following steps.

Mathematical Induction Examples

Question 1 :

By the principle of mathematical induction, prove that, for n ≥ 1

1² + 3² + 5² + · · · + (2n − 1)² = n(2n − 1)(2n + 1)/3

Solution :

Let p(n) =  1² + 3² + 5² + · · · + (2n − 1)² = n(2n − 1)(2n+1)/3

Step 1 :

put n = 1

p(1)  = 1² + 3² + 5² + · · · + (2(1) − 1)² = 1(2(1) − 1)(2(1)+1)/3

  1  =  1

Hence p(1) is true.

Step 2 :

Let us assume that the statement is true for n = k

p(k) = 1²+3²+5²+ · · · + (2k − 1)² = k(2k − 1)(2k+1)/3  ---(1)

We need to show that P(k + 1) is true. Consider,

Step 3 :

Let us assume that the statement is true for n = k + 1

p(k+1) 

1² + 3² · · · + (2(k+1) − 1)² = [(k+1)(2(k+1) − 1)(2(k+1)+1)]/3 

1² + 3² · · · + (2k+1)² = [(k+1)(2k + 1) (2k + 3)]/3 

1² + 3² · · · + (2k-1)² + (2k+1)² = [(k+1)(2k + 1) (2k + 3)]/3 

By applying (1) in this step, we get

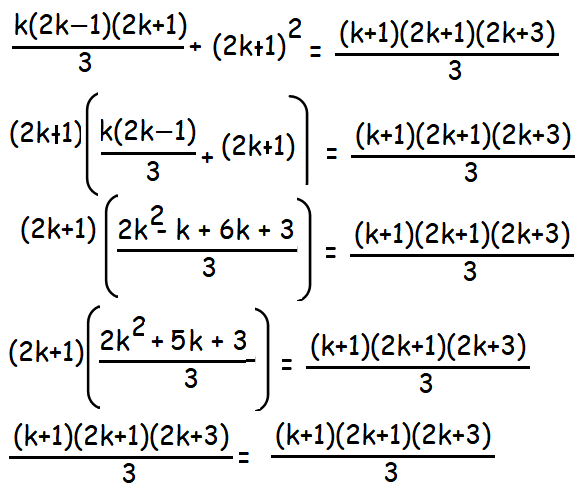
Hence, by the principle of mathematical induction,n ≥ 1

1² + 3² + 5² + · · · + (2n − 1)² = n(2n − 1)(2n + 1)/3

Question 2 :

Prove that the sum of the first n non-zero even numbers is n² + n.

Solution :

Let p(n) be the statement "n² + n" is even.

Step 1 :

p(n)  =  n² + n

put n = 1

p(1)  =  1² + 1  =  2, which is even

Hence p(1) is true.

Ste 2 :

Let p(m) is true. Then 

p(m) is true  ==>  m² + m is even ==>  m² + m  ==> 2λ for some λ ∊ N

Now, we shall show that p(m + 1) is true. For this we have to show that (m+1)² + (m + 1) is an even natural number.

Now,

(m+1)² + (m + 1)  =  m² + 2 m + 1 + m + 1

  =  m² + 2 m + m + 2

  =  m² + m + 2m + 2

  =  m² + m + 2(m + 1)

  =  2λ + 2 (m + 1)

  =  2(λ + m + 1)

Hence p(m + 1) is true.

Hence the sum of the first n non-zero even numbers is n² + n.

After having gone through the stuff given above, we hope that the students would have understood "Mathematical Induction Examples". 

Apart from the stuff given above, if you want to know more about "Mathematical Induction Examples". Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.