MATH SYMBOLS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
To do various operations in Math, symbols can be used. The most advantage of using symbols in math is to make a lengthy verbal phrase in simple manner. For example, the verbal phrase "addition of a and b" can be written using the symbol '+' as given below.
a + b
In this way, we can write many different operations can be written in a simple manner using symbols.
More Examples :
4 is decreased by y : 4 - y
5 times y added to 3 times x : 3x + 4y
x divided 7 times y : 4 ÷ 7y
Common Math Symbols
Set Theory Symbols
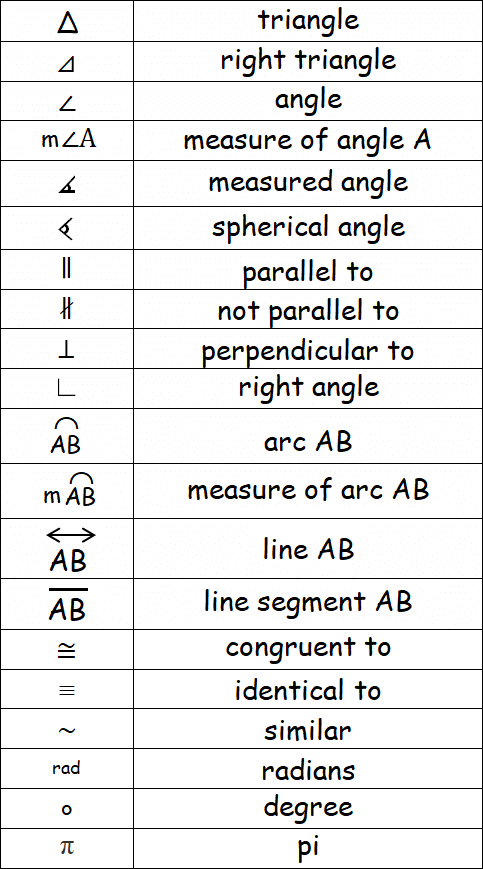
Geometry Symbols
Statistics Symbols
Calculus Symbols
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Practice Test with Answers (Part - 2)
Apr 13, 26 06:21 PM
Digital SAT Math Practice Test with Answers (Part - 2) -
Digital SAT Math Questions and Answers (Part - 13)
Apr 13, 26 12:18 PM
Digital SAT Math Questions and Answers (Part - 13) -
SAT Math Resources (Videos, Concepts, Worksheets and More)
Apr 09, 26 07:46 PM
SAT Math Resources (Videos, Concepts, Worksheets and More)
