MATH WORKSHEET FOR CLASS 9 WITH SOLUTIONS

Problem 1 :

For every real number x, does x² - 1

(A)  > 0   (B)  < 0   (C)  = 0

Solution  :

x² - 1²

(x - 1)(x + 1)

Since x is real value, we can take all positive and negative values of x.

So, the answer is < 0.

Problem 2 :

If two sides of a triangle are equal, then the angles opposite to them are

(A)  Not Equal   (B)  Equal   (C)  Supplementary

Solution :

By isosceles triangle theorem,

If two sides of a triangle are equal, then the angles opposite to these sides are equal.

So, the answer is Equal.

Problem 3 :

The sum of the digits of the two digit number is 8. If the digits are reversed the number is increasing by 18. Find the number.

(A)  33   (B)  20   (C)  35

Solution :

Let the two digit number be xy

Sum of two digit numbers,

x + y  =  8 ----(1)

Expand form,

xy  =  10x + y

yx  =  10y + x

Digits are reversed the number is increasing by 18,

10y + x  =  10x + y + 18

10y  =  10x + y + 18

9y - 9x  =  18

y - x  =  2 ----(2)

Add (1) and (2), we get

x + y + y - x  =  8 + 2

2y  =  10

y  =  5

By applying y  =  5 in equation (1), we get

x + 5  =  8

x  =  3

So, the number xy is 35

Problem 4 :

If the slope of the line is not defined, then the line is

(A)  Falling line   (B)  Parallel to x-axis   (C)  Parallel to y-axis

Solution :

If the Slope of a line is not defined, then the line is parallel to y-axis.

So, the answer is parallel to y-axis.

Problem 5 :

The slope of the line passing through (5, 6) and (15, 9) is

(A)  -3/8   (B)  4/9   (C)  3/10

Solution :

Given points, (5, 6) and (15, 9)

Using Two Point form :

Slope  =  (y₂ - y₁)/(x₂ - x₁)

(5, 6) -----> (x₁, y₁)

(15, 9) -----> (x₂, y₂)

Slope  =  (9 - 6)/(15 - 5)

Slope  =  3/10

So, the answer is 3/10

Problem 6 :

What is the x-intercept and y-intercept of the line 3x + 4y  =  12 ?

(A)  (2, 1)   (B)  (4, 3)   (C)  (6, 8)

Solution  :

Given, 3x + 4y  =  12

Finding x-intercept :

When y  =  0

3x + 4(0)  =  12

3x  =  12

x  =  4

Finding y-intercept :

When x  =  0

3(0) + 4y  =  12

4y  =  12

x  =  3

So, the answer is (4, 3)

Problem 7 :

Find the equation of the line having slope 21 and y-intercept -3.

(A)  2x + y  =  0   (B)  x + 2y  =  0   (C)  21x - y - 3  =  0

Solution :

Using Slope-intercept form :

y  =  mx + b

Here m  =  21 and b  =  -3

y  =  21x - 3

21x - y - 3  =  0

Problem 8 :

If sin θ  =  7/25, then the value cot θ is

(A)  10/27   (B)  21/35   (C)  24/7

Solution :

We know that,

sin²θ + cos²θ  =  1

We have, sin θ  =  7/25

(7/25)² + cos²θ  =  1

49/625 + cos²θ  =  1

cos²θ  =  1 - 49/625

cos²θ  =  576/625

cos θ  =  24/25

Now,

cot θ  =  cos θ/sin θ

=  24/25 × 25/7

=  24/7

So, the answer is 24/7.

Problem 9 :

Find the median of the numbers 23, 25, 29, 30, 39

(A)  29   (B)  20   (C)  31

Solution :

Given data 23, 25, 29, 30, 39 in ascending order.

So, Median  =  Middle value

=  29

So, the answer is 29

Problem 10 :

Find the compound interest on $64,000 for 1 year at the rate of 10% per year compounded quarterly.

(A)  $6644.03  (B)  $4921   (C)  $421

Solution :

Given, 

Principal (p)  =  $64000

Rate (r)  =  10%  =  10/4% (for Quarterly)

Time  =  1 year  =  1 × 4  =  4(for Quarterly)

By using this formula,

Amount  =  P(1 + R/100)ⁿ

=  64000[1 + (10/4 × 1/100)]⁴

=  64000[1 + 10/400]⁴

=  64000[410/400]⁴

=  64000[1.025]⁴

=  64000[1.1038]

Amount  =  $70644.03

Compound interest  =  Amount - Principal

=  70644.03 -  64000

=  $6644.03

Problem 11 :

Which expression is equivalent to √184

a)  92    b) 2√46     c)  4√23     d) 4√46

Solution :

= √184

Decomposing using prime factorization, we get

= √2⋅2⋅2⋅23

= 2√2⋅23

= 2√46

Problem 11 :

The graph of a linear function is shown on the grid

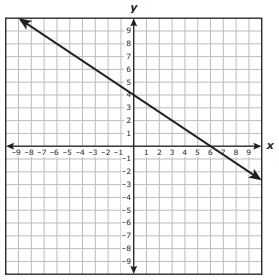
Write the equation of the line shown above.

Solution :

Slope = 2/3

Since it is the falling line, its slope must be negative.

Slope of the line = -2/3

y-intercept = 4

y = mx + b

y = (-2/3) x + 4

y = (-2x + 12)/3

3y = -2x + 12

2x + 3y = 12

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.