MATH TEST FOR GRADE 10 WITH MIXED TOPICS

Problem 1 :

Find the indicated term of the sequence if

a_n = 5 + 2 (n-1) then a₇ 

Solution :

We have nth term or general term of the sequence.

a_n  =  5 + 2 (n-1)

a₇  =  5 + 2(7-1)

  =  5 + 2(6)

  =  5 + 12

a₇  =  17

Problem 2 :

Find the equivalent form of (A ∪ B)' =  

 (A) (A' ∪ B')     (B) (A ∪ B')      (C) A' ∩ B'

Solution :

(A ∪ B)'  =  A' ∩ B' 

Problem 3 :

Find the sum of the volumes of 15 cubes,whose sides are 1 cm, 2 cm, 3cm ,........ 15 cm respectively.

Solution :

Volume of cubes given above is

1³ + 2³ + 3³ + ......... + 15³

Sum of cube  =  [n(n + 1)/2]²

n  =  15

=  [15(15 + 1)/2]²

=  [15(16)/2]²

  =  [15(8)]²

=  120²

=  14400

Sum of volume of the above cubes is 14400 cm³

Problem 4 :

It is 9 hours now in a 12 hour clock What was the time 71 hours back ?

Solution :

Step 1 :

Subtract 71 from 9.

That is,

9 - 71  =  -62

Step 2 :

We get negative value in step 1 and also 62 is not divisible by 12.

So, find the next integer after 62 which is exactly divisible by 12.

That is 72.

Step 3 :

Write -62 in terms of 72.

So, -62 can be written as

-62  =  -72 + 10

Therefore, the time 71 hours back was 10 hours.

Problem 5 :

A vessel is in the form of a hemispherical bowl mounted by a hollow cylinder. The diameter of hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the volume.

Solution :

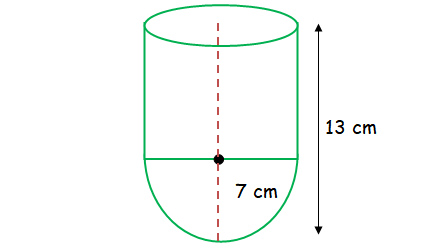
Height of vessel  =  13 cm

radius of hemisphere + height of cylinder  =  13

7 + h  =  13

h  =  13 - 7  =  6 cm

Volume of vessel 

  =  volume of hemisphere + volume of cylinder

  =  (2/3)πr³ + πr² h

  =  πr²[(2/3) r + h]

  =  (22/7) 7²[(2/3) 7 + 6]

  =  (22/7) 49 (32/3)

  =  1642.67 cm³

Problem 6 :

A conical piece of lead has a radius of 5.25 cm and is 8 cm is height. If it is melted and made into smaller cones 2 cm high and 1.75 cm in diameter, find how many such cones can be made.

Solution :

radius of lead (R) =  5.25 cm and height(H)  =  8 cm

Diameter of cone  =  1.75, radius (r)  =  1.75/2

height of cone(h)  =  2 cm

Volume of conical piece of lead  =  n (Volume of cone)

(1/3)πR² H  =  (1/3) πr² h

(5.25)² ⋅ 8  =  n (1.75/2)² ⋅ 2

n  =  220.5/1.53

n  =  144

So, the number of small cones is 144.

Problem 7 :

Find the sum and product of roots of the quadratic equation given below. 

3x² + x + 1  =  0

Solution :

Comparing

3x² + x + 1  =  0

and 

ax² + bx + c  =  0

we get

a  =  3, b  =  1 and c  =  1

Therefore, 

Sum of the roots  =  -b/a  =  -1/3

Product of the roots  =  c/a  =  1/3

Problem 8 :

Find the square root of

(4x² − 9x + 2) (7x² - 13x - 2) (28x² - 3x - 1).

Solution :

  =  √(4x² − 9x + 2) (7x² - 13x - 2) (28x² - 3x - 1)

4x² − 9x + 2  =  (4x - 1)(x - 2)

7x² - 13x - 2  =  (7x + 1)(x - 2)

28x² - 3x - 1  =  (4x - 1) (7x + 1)

  =  √(4x - 1)(x - 2)(7x + 1)(x - 2)(4x - 1) (7x + 1)

  =  |(4x - 1)(x - 2)(7x + 1)|

The sum of the digits of a two digit number is 10. If the number formed by reversing the digits is less than the original number by 36,find the required number.

  (A) 73      (B) 55      (C) 64           (D) 28

Solution :

Let "x y" be the required two digit number. Here "x" is in ten's place and "y" is in unit place.

The sum of the digits of a two digit number  =  10

x + y  =  10  --------(1)

If the number formed by reversing the digits is less than the original number by 36.

 y x  =  x y - 36

Let us write these as expanded form

10 y + x = 10 x + y - 36

x - 10 x + 10 y - y = - 36

- 9 x + 9 y = - 36

By divide this equation by 9 we will get

- x + y = -4  --------(2)

  (1) + (2)    x + y = 10

                -x + y = -4

                _________

               2 y = 6  ==>  y = 3

By applying y = 3 in (1), we get

x + 3  =  10

x  =  7

Therefore the required number is 73.

Problem 10 :

How far is a chord of length 10 cm from the center of a circle of radius 13 cm.

Solution :

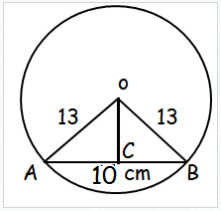
In triangle OCB,

OB²  =  OC² + CB²

OC bisects the chord.

13²  =  OC² + 5²

OC²  =  169 - 25

OC²  =  144

OC  =  12 cm

So, the distance between center and the chord is 12 cm.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.