MATH TERMS THAT START WITH Q

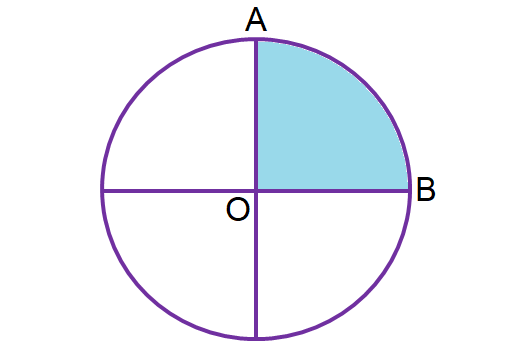
Quadrant :

A sector one quarter of a circle , or sector of a two dimensional Cartesian coordinate system.

Quadratic equation :

A polynomial with second degree is called quadratic equation.

General form of a quadratic equation is ax²+bx+c  =  0.

Here a, b and c are real numbers.

Quadrilateral :

A polygon with four sides and four angles. Square, rectangle, rhombus, parallelogram, kite, trapezium all are some forms of quadrilaterals.

Quadruple :

A number four times greater as another. That is to multiply or increase by four times.

Qualitative :

Descriptions or distinctions based on some qualities or characters.

Quantity :

A particular or infinite amount of anything.

Example :

A small quantity of milk.

Quarter :

One fourth of a quantity. One fourth of Canadian and American dollar. It has been written as 1/4.

Quartic :

Polynomial of degree 4 is called quartic.

Example :

4x⁴ + 3x³ + 2x² - 5x + 1

Quartiles :

In statistics, quartiles are the three points that divide the data into four equal parts. Median, lower quartile and upper quartile are those three points.

Quintic :

A polynomial(function) of degree 5 is called quintic function.

Example :

x⁵-x⁴- 2x³-x²+5

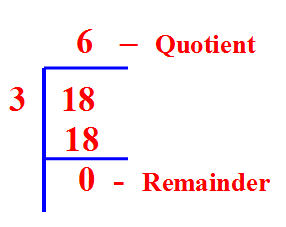
Quotient :

The result of division. The number of times one quantity is contained in another.

Example :

The quotient of of 6 divided by 3 is 2.

Quadratic Equation :

If the highest power of the variable in any equation is 2.Then we can that equation is quadratic equation. The general form of any quadratic equation is ax²+ bx + c = 0.

Quadratic Formula :

The formula to be used to solve the quadratic equation.

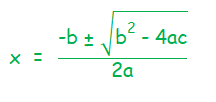
Quotient Rule :

This is the formula to be used to differentiate two x related functions which are multiplying.

(U/V)' =  [VU'-UV']/V²

Quintuple :

Multiplying any number by a factor of 5.

Quintiles :

From a set of data, the 20th and 80th percentiles are called the quintiles.

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.