MATH TERMS THAT START WITH A
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Addition :
One of the four basic operations in arithmetic and algebra. By adding two (or more) numbers we determine the sum of those numbers.
Addition Property of Equality :
Let A, B and C be any algebraic expressions. If A = B, then
A + C = B + C
Addition Property of Inequalities :
Let A, B and C be any algebraic expressions. If A ≤ B, then
A + C ≤ B + C
Additive Identity :
An element e of some set S, that has the property
a + e = a
for any element a. In the number system (real or complex), e = 0.
Additive Inverse :
For a given element a of some set S, the element b with the property a + b = e, where e is the additive identity. In the number system (real or complex), e = 0 and b = -a.
Adjacent Angle :
Two angles that have common vertex, one common side but no common interior points.
Adjacent Side :
Any of two sides in a triangle which make up the angle, are called adjacent. The other side of the same triangle is the opposite side. In the trigonometry of right triangles, this term is reserved for one side of acute angle only, namely the side which is the leg, not the hypotenuse of the triangle.
Algebra :
One of the main branches of mathematics, that deals with numbers, variables, equations, etc. and operations with them. In a more general setting, the developments of classical algebra, namely linear algebra and abstract algebra, deal with vectors, matrices and structures such as groups, rings, fields and others.
Algebraic Equation :
An equation involving just algebraic function. Most common example is an algebraic equation involving a polynomial :
P(x) = 0
where P(x) is a polynomial of one or n variables respectively. Example :
3x2 - 5x - 2 = 0
Algebraic Expression :
An expression which involves numeric constants, one or more variables and only the algebraic operations of addition, subtraction, multiplication, division, and root extraction.
Algebraic Function :
A function that involves the algebraic operations of addition, subtraction, multiplication, division, and root extraction. The function
f(x) = x4 + 3x3 - 5x2 + 7x - 5
is an algebraic function but g(x) = log(sin x) is not.
Algebraic Number :
A complex number z is an algebraic number if it satisfies a non-trivial polynomial equation P(z) = 0 for which the coecients are rational numbers. It is known that many irrational numbers are not algebraic, in particular numbers π and e. These kind of numbers are called transcendental.
Algebraic Operation :
One of the basic operations of algebra : addition, subtraction, multiplication, division, or root extraction.
Algorithm :
A method or procedure of solving a given problem or whole class of problems by a limited number of standard operations.
Alternate Angles :
When two parallel lines are crossed by the third one (called a transversal), eight angles are formed. Two pairs of non-adjacent interior angles are called alternate. Alternate angles are always equal. In picture below pairs ∠3 and ∠5 and ∠4 and ∠6 are alternating angles.
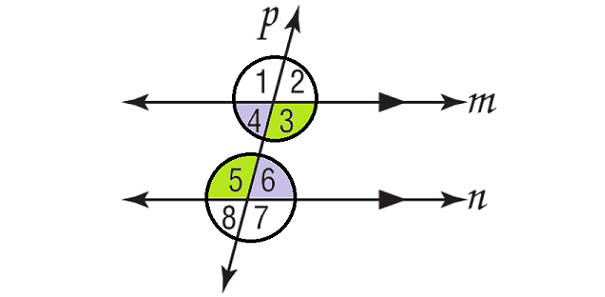
Alternating Series :
A numeric series where the successive terms have opposite signs.
Example :
1 - 2 + 4 - 8 + .......
Altitude of a Triangle :
The perpendicular segment from any vertex of a triangle to the opposite side (or its continuation). Depending on the type of triangle (acute, right, obtuse), the altitude may or may not be inside the triangle.
In the triangle shown below, AD is the altitute.
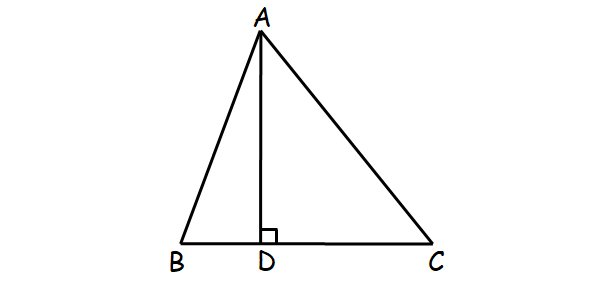
Analytic Geometry :
One of the branches of geometry. Analytic geometry combines the geometric and algebraic methods by introducing coordinate systems, and presenting geometric objects with the help of algebraic functions and their graphs.
Angle :
Geometric object, which consists of a point, called vertex and two rays coming out of this point. In trigonometry and calculus, angles usually are placed in standard position, when the vertex is placed at the origin of the Cartesian coordinate system, one side, called initial, coincides with the positive half of the x-axis and the other side, called terminal, can have arbitrary direction. In this position angles can be both positive and negative. The angles, where the terminal side is moved counterclockwise, are con sidered positive and clockwise direction is considered
negative.
The two main measuring units for angles are the degree measure and the radian measure. Two angles with the same terminal side are called coterminal and they differ in size by an integer multiple of a full circle, i.e. by multiple of 360° or 2π, depending on measuring unit. Angles traditionally are classified by their measure: An angle between 0 and 90 degrees is called acute, a 90 degree angle is called right, between 90 and 180 degrees - obtuse and 180 degrees - straight. Additionally, angles measuring 90, 180, 270 or 360 degrees are called quadrantal.
Angle Bisector :
A ray, coming out of the vertex of an angle, that divides the given angle into two equal parts. In the triangle shown below, AD is the angle bisector of ∠A.
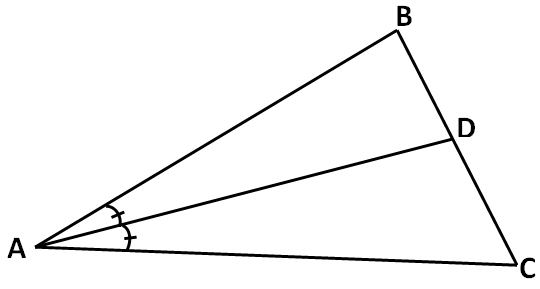
Angle of Elevation :
If an object is viewed from below, then the angle between the horizontal line and the line drown between the viewer and the object, is the angle of elevation.
Angle of Depression :
If an object is viewed from above, then the angle between the horizontal line and the line drown between the viewer and the object, is the angle of depression.
Arithmetic :
The earliest and most fundamental branch of mathematics. Arithmetic deals with numbers and arithmetic operations on them: addition, subtraction, multiplication and division. In a more modern and wider sense, the term arithmetic is also used as a synonym to number theory, which is the only part of arithmetic still subject to research activity.
Arithmetic Mean or Average :
For a positive integer n, and given real numbers
a1, a2, a3, ..... an,
the arithmetic mean is
Arithmetic Expression :
An expression which involves numeric constants and the arithmetic operations of addition, subtraction, multiplication, division, and natural exponents.
Example :
Arithmetic Sequence or Progression :
A sequence of real numbers where the diference between two consecutive terms is the same.
Example :
2, 7, 12, 17, ........
Associative Property :
For addition : for any numbers a, b, c complex or real,
a + (b + c) = (a + b) + c
For multiplication : for the same three numbers,
a x (b x c) = (a x b) x c
Axiom :
A statement that is assumed to be true without proof, and used as a basis for proving other statements, less obvious. Also is called postulate.
Axis :
In Cartesian coordinate system, the name of lines that are used to calculate the position of a point in two, three or higher dimensional spaces. See also x-axis, y-axis, z-axis. The x-axis is also called abscissa and real axis and the y-axis is called ordinate and imaginary axis.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com
Recent Articles
-
10 Hard SAT Math Questions (Part - 40)
Dec 18, 25 06:27 PM
10 Hard SAT Math Questions (Part - 40) -
Digital SAT Math Problems and Solutions (Part - 13)
Dec 18, 25 12:26 PM
Digital SAT Math Problems and Solutions (Part - 13) -
90 Degree Clockwise Rotation
Dec 18, 25 09:42 AM
90 Degree Clockwise Rotation - Rule - Examples with step by step explanation

