MATH TERMS STARTING WITH E

e :

It is an important mathematical constant approximately equal to 2.71828. Other names are Euler's number or Euler's constant after the famous mathematician Leonhard Euler. Some times it is also known as Napier's constant. It is denoted in limit form as    

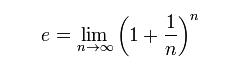
Eccentricity :

In math, eccentricity is a parameter associated with conic section, that is how much the conic section deviates from being a circle. Eccentricity is denoted by 'e' or 'ε'.

• The eccentricity of a circle is 0.
• The eccentricity of ellipse is 0 < e < 1.
• The eccentricity of parabola is 1.
• The eccentricity of hyperbola is greater than 1.

Edge :

A line that connects two vertices of a polygon. In the shape cube we have 12 edges.

Element :

A member or constituent of a set. For example 'a' is an element of the set {a, b, c, d}

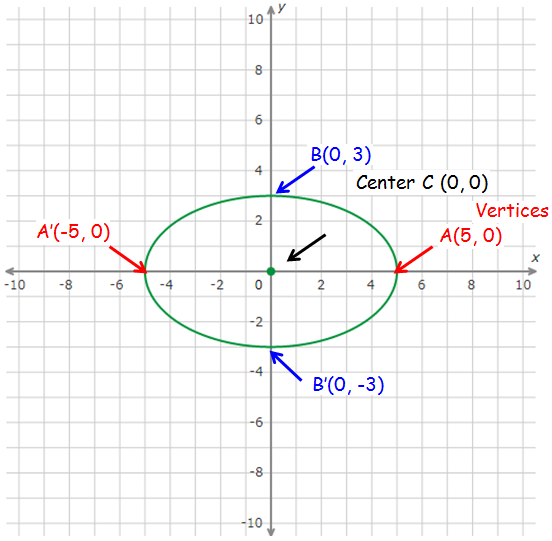
Ellipse :

In conic section an ellipse is a smooth closed curve which is symmetric about its horizontal and vertical axes.

End point :

The point at which a line or a ray terminates or ends.

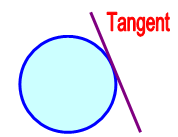
Equation of tangent :

A tangent to a circle is a straight line which intersects (touches) the circle exactly one point. We can draw only two tangents to a circle from the point outside to a circle.

To get the equation of a tangent at(x₁, y₁) we have to replace x²  by xx₁,  y² by yy₁ , x as (x + x₁)/2 and y as (y + y₁)/2 in the equation of a circle.

Equation of the straight line :

A linear equation or an equation of the first degree in x and y represents a straight line.The equation of a straight line is satisfied by the co-ordinates of every point lying on the straight line and not by any other point outside the straight line. 

(i)  Slope intercept form : 

y  =  m x + b

Here m = slope and b = y-intercept

(ii) Two point form :

(y - y₁)/(y₂ - y₁)  =  (x - x₁)/(x₂ - x₁)

Here (x₁, y₁) and (x₂, y₂) are the points on the line.

(iii)  Point Slope form:

(y - y₁)  =  m (x - x₁)

Here m  =  slope and (x₁, y₁) are the given point on the line.

(iv)  Intercept form :

(x/a) + (y/b)  =  1

Here a = x-intercept and b = y-intercept

Equation :

An equation is a condition on variable.

And also it is an algebraic expression in which each term is a constant or with a product of a variable.

Equation of circle :

There are three ways to find equation of any circle

(i)  Equation of the circle when the center at origin and radius as r.

x² + y²  =  r²

(ii)  Equation of the circle when the center at (h, k) and radius as r.

(x - h)² + (y - k)²  =  r²

(iii) Equation of the circle if the end points of a diameter are given

(x - x₁)(x₂ - x₁) + (y - y₁)(y - y₂)  =  0

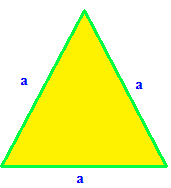
Equilateral triangle :

A shape which is covered by three equal sides is called Equilateral triangle.

Exponent :

Exponent of a number shows you how many times the number is to be used in a multiplication.

For example 2 x 2 x 2 x 2 x 2 can be written as 2⁵, we read it as “Two raised to the power 5” or fifth power of two, or we can say simply 2 to the power five.

Equal sets :

Two sets A and B are said to be equal if they have same elements. That is every element in A must be the element of B and every element of B must be the element of A.

For example

•           A  =  Set of vowels.
•           B  =  {a, e, i, o, u}.

here both sets are having the same elements. So A and B are equal sets. That is A  =  B.

Equal sets :

Two sets A and B are said to be equivalent if they have the same cardinal number. That is, the number of elements in both A and B should be the same. The symbol to denote two equivalent sets is '↔'.

For example

• A  =  Set of all colors in pencil box.
• B  =  Set of all days in week.

Here n(A)  =  7 and n(B)  =  7, so both A and B are equivalent sets. That is, A↔B.

These are the types in types of set.

Empty set :

A set which contains no element is called as empty set or null set. It is also called as void set or vacuous set. Empty set is denoted by the Greek symbol φ, which is read as 'phi'. In Roster form it is denoted by { }.

Equivalent fractions :

Equivalent fractions are fractions that represent the same value or same part of an object.

Consider the below fractions.

1/2, 2/4, 3/6, 4/8, 5/10

Each fraction represent same value 1/2. So these are equivalent to each other.

Euler's Theorem :

If f(x,y) is a homogeneous function of degree n,then

x (∂f/∂x) + y(∂f/∂y) = n f

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.