MATH QUESTIONS FOR GRADE 7 WITH ANSWERS

Question 1 :

A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the length of broken part.

(A)   13 m        (B)  15 m    (C)  18 m

Solution :

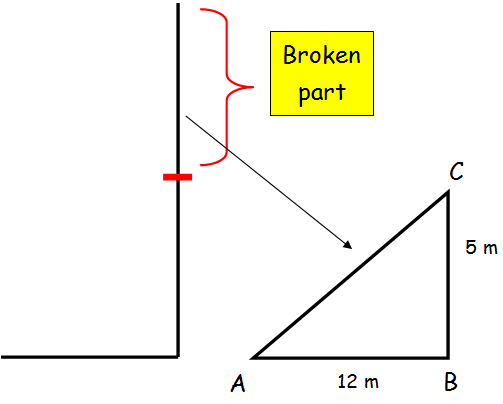
Here,

AC²  =  AB² + BC²

AC²  =  12² + 5²

AC²  =  144 + 25  ==>  169

AC  =  √169  =  √13 ⋅ 13

AC  =  13 m

So, the length of the broken part is 13 m.

Question 2 :

Find the ratio of 3 km to 300 m.

(A)  10:1            (B)  1:10              (C)  2:5

Solution :

We can compare two ratios of the same kind only.So,let us convert km to meters.

1000 m  =  1 km

3 km  =  3 x 1000  =  3000 m

  =   3000 :  300

  =   10 : 1

So, the required ratio is 10 : 1.

Question 3 :

Find BC, if the area of the triangle ABC is 36 cm² and the height AD is 3 cm.

(A)  18 cm            (B)  24 cm              (C)  10 cm

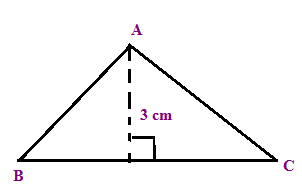
Solution :

BC =  Base of the triangle

AD  =  Height of the triangle  =  3 cm

Area of triangle  =  (1/2) x Base x Height

  =  (1/2) x BC x AD

36  =  (1/2) x BC x 3

(36 ⋅ 2)/3  =  BC

BC  =  24 cm 

So, the base of the triangle is 24 cm.

Question 4 :

How many times a wheel of radius 28 cm must rotate to go 352 m? (Take π = 22/7) 

(A)  300 times        (B)  200 times        (C)  400 times

Solution :

Radius of wheel  =  28 cm

Distance to be covered  =  352 m  =  35200 cm

Distance covered in one revolution  =  2πr 

  =  2 ⋅ (22/7) ⋅ 28 

=  176 cm

Number of revolutions 

=  Distance to be covered/Distance covered in one revolution

=  35200/176 

  =  200 times

So, the wheel has to be rotated 200 times to go 352 m.

Question 5 :

A rectangular park is 45 m long and 30 m wide. The path 2.5 m wide is constructed outside the park. Find the area of that path.

(A)   400 m²    (B)  200 m²   (C)  150 m²

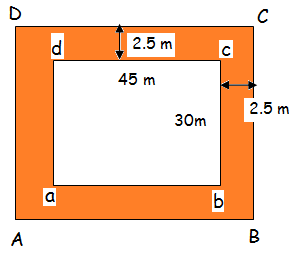
Solution :

Area of path 

=  Area of rectangle ABCD - Area of rectangle abcd

Area of path  = 50 ⋅ 35 -  45 ⋅ 30 

  =  1750  -  1350 

  =  400 m² 

So, the area of the path is 400 m² .

Question 6 :

Find the value of the expression a² + 2 ab + b²  

if a = 3, b = 2

(A)   27        (B)  35            (C)  25

Solution :

a² + 2 ab + b²   =  3² + 2 (3)(2) + 2²

=  9 +  12 + 4

=  25

So, the value of the given expression is 25.

Question 7 :

In a computer lab, there are 3 computers for every 6 students. How many computers will be needed for 24 students?

(A)   27        (B)  35            (C)  25

Solution :

There are 3 computers for every 6 students

Number of computers for 1 student  =  3/6  =  1/2

Number of computers for 24 students  =  (1/2) 24

  =  12 computers

So, every 24 students need 12 computers.

Question 8 :

The side of an equilateral triangle is 3.5 cm. Find its perimeter.

(A)  5.9 cm      (B)   2.7 cm     (C)  10.5 cm

Solution

Side length of equilateral triangle  =  3.5 cm

Perimeter of equilateral triangle  =  3a

  =  3 (3.5)

  =  10.5 cm

So, the perimeter of the equilateral triangle is 10.5 cm.

Question 9 :

Find the value of 2.5 + 5.1

(A)  7.6      (B)   2.5     (C)  8.2

Solution

oooooooooooooooooooooo2.5 (+) ooooooooooooooooooooooo

oooooooooooooooooooooo5.1ooooooooooooooooooooooooooo

oooooooooooooooooooo_____ooooooooooooooooooooooooo

oooooooooooooooooooo07.60000oooooooooooooooooooooo

oooooooooooooooooooo_____ooooooooooooooooooooooooo

Question 10 :

The wood cutter took 12 minutes to make 3 pieces of a block of wood. How long would be needed to make 5 such pieces? 

(A)  50 minutes       (B)  20 minutes      (C)   30 minutes

Solution :

Time taken for wood cutter to cut block of wood into 3 pieces  =  12 minutes

Time taken for wood cutter to cut a block of wood into 1 piece

  =  12/3  =  4 minutes

Time taken for wood cutter to cut a block of wood as 5 pieces

  =  4 (5)  =  20 minutes

So the time taken is 20 minutes.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.