MATH PRACTICE TEST FOR 9th GRADE

Problem 1 :

Find the area of the design as shown below.

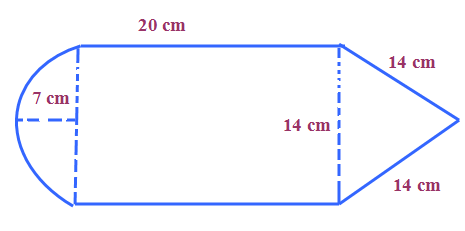
Solution :

Area of rectangle  =  l x b

Area of semicircle  =  πr²/2

Area of equilateral triangle  =  (√3/4)⋅a²

  =  πr²/2 + l x b + (√3/4)⋅a²

  =  (1/2)⋅(22/7)⋅7² + 20 ⋅ 14 + (√3/4)⋅14²

=  441.368 cm²

Problem 2 :

A cow is tied to one of the corners of a square-shaped field of sides of 10 m. The length of the rope is 7 m. How would one find the area of the field that the cow cannot graze?

Solution :

Area of square field  =  10²

Area of the filed that cow can graze  =  πr²/4

  =  (1/4) ⋅ (22/7) ⋅ 7 ⋅ 7

=  77/2

Area of the filed that cow can graze  =  100 - 77/2

=  61.5 m²

Problem 3 :

Write the number 0.000001024 in scientific notation

Solution :

0.000001024  =  1.024 x 10⁶

Problem 4 :

Write the number 1.423 × 10^-6 in decimal form.

Solution :

  =   1.423 × 10^-6 

  =  1.423/1000000

  =  0.000001423

Problem 5 :

Perform the calculation and write the answer of the following in scientific notation.

(2000)² ÷ (0.0001)⁴

Solution :

(2000)² ÷ (0.0001)⁴

  =  (2x10³)² ÷ (1x10^-4)⁴

  =  (4x10⁶) ÷ (1x10^-16).

  =  4x10⁶⁺¹⁶

  =  4x10²²

Problem 6 :

Solve for x

3  =  log_x729

Solution :

x³  =  729

x³  =  3⁶

x³  =  (3²)³

x  =  9

So, the value of x is 9.

Problem 7 :

Change 2  =  64¹⁶ to logarithmic form.

Solution :

2  =  64¹⁶ 

log₆₄ 2  =  16

Problem 8 :

Evaluate 

log₉ (1/27)

Solution :

log₉ (1/27)

=  log₉ (1/3)³

=  log₉ 3^-3

=  -1log₉ 3

=  -1/log₃9

=  -1/log₃3²

=  -1/2log₃3

=  -1/2

So, the answer is -1/2.

Problem 9 :

How many integers between 100 and 999, inclusive, have the property that some permutation of its digits is a multiple of 11 between 100 and 999 For example, both 121 and 211 have this property.

Solution :

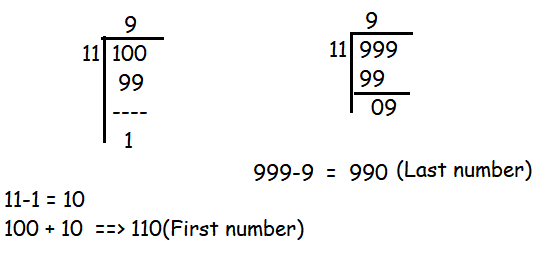
110, 121, .........990

n  =  [(l-a)/d]+1

n  =  (990-110)/11 + 1

n  =  (880/11) + 1

n  =  81

Number of three digit numbers divisible by 11 is 81.

Each number will consist of three digits, using these three digits we can make 6 possible 3 digit numbers.

81 x 6  =  486

In 486 numbers we have repeated counting.

For example, the number abc is divisible by 11, then cba is also divisible by 11. (Divisibility rule for 11)

So, 486/2  =  243

In those 243 numbers, we may have numbers consisting of one zero.

110, 220, 330, 440, 550, 660, 770, 880, 990

In this way, we can get 9 numbers. If we use the digits in the different places, that will not be divisible by 11 or it must a two digit number.

If the middle digit is 0, then

209, 307, 407, 506 by reversing the digits we will get 902, 703, 704, 605. So 8 numbers.

  =  243 - (9+8)

  =  226

Problem 10 :

Obtain the set builder representation of the set

  A  =  {1, 1/2, 1/3, 1/4, 1/5, 1/6}

Solution :

A  =  {x: x  =  1/n where n is a integer}

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.