MATCHING THE PROPERTY OF RATIONAL NUMBER QUIZ

Properties of Rational Numbers

Matching the Property of Rational Number Quiz

Question 1 :

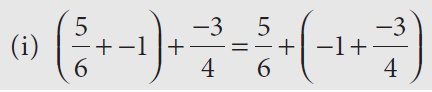
Solution :

The given statement exactly matches the general form (a + b) + c  =  a + (b + c).

It is in the associative property of addition.

Question 2 :

Solution :

The given statement is in the form a x (b + c)  = (a x b) + (a x c)

The name of the property is distributive property of multiplication over addition.

Question 3 :

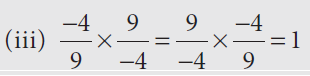
Solution :

If a = -4/9, 1/a  =  9/(-4)

a x (1/a)  =  1

Hence the given is inverse property of multiplication.

(iv)  1/0

Solution :

It is undefined.

(v)  22/7

Solution :

If is a rational number.

Question 4 :

Which of the following properties hold for subtraction of rational numbers? Why?

(a) closure (b) commutative (c) associative

(d) identity (e) inverse

Solution :

Closure property :

For any two rational numbers a and b, we may get 

Commutative property :

a - b ≠  b - a

Associative property :

a - (b - c) ≠ (a - b) - c

Inverse property :

Inverse property fails.

Identity property :

5 - 0 ≠ 0 - 5

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.