MAKING A SCATTER PLOT WORKSHEET
Question 1 :
The final question on a science test reads, how many hours spent studying for this test. The teacher records the number of hours each student studied and the marks scored by the respective student on the test.
Hours Spent for Studying
0
0.5
1
1
1.5
1.5
2
3
4
Marks Scored by the Students
75
80
80
85
85
95
90
100
90
Describe the type of association between number of hours spent for studying and marks scored using scatter plot.
Question 2 :
What trend can we see in the data given in question 1 ?
Question 3 :
Can we conclude the grade associated with studying for 10 hours would follow the trend in question 2 ?
Question 4 :
Can we say the relationship given in question 1 as positive or negative ?
Question 5 :
The scatter plot shows David’s height at various ages. Describe the type of association between David’s age and his height. Explain.
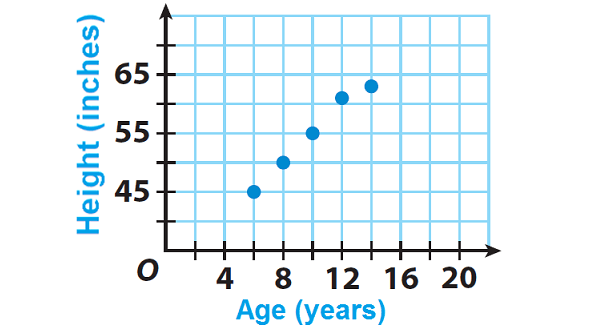
Question 6 :
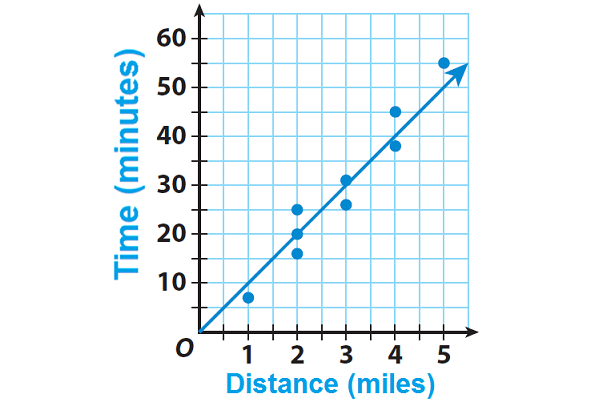
Alexa is training for a 10K race. For each of her training runs, she recorded the distance she ran and the time she ran. She made a scatter plot of her data and drew a trend line. Use the trend line to predict how long it would take Alexa to run 4.5 miles.
Detailed Answer Key
Question 1 :
The final question on a science test reads, how many hours spent studying for this test. The teacher records the number of hours each student studied and the marks scored by the respective student on the test.
Hours Spent for Studying
0
0.5
1
1
1.5
1.5
2
3
4
Marks Scored by the Students
75
80
80
85
85
95
90
100
90
Describe the type of association between number of hours spent for studying and marks scored using scatter plot.
Answer :
Step 1 :
Make a prediction about the relationship between the number of hours spent studying and marks scored.
When we look at the above data, we can make the following prediction. A greater number of study hours are likely to be associated with higher marks.
Step 2 :
Make a scatter plot. Graph hours spent studying as the independent variable and marks scored by the students as the dependent variable.
Moreover, if we consider hours spent for studying as variable "x" and marks scored by the students as variable "y", we can write the above data as ordered pairs in the form (x, y).
Then, we have
(0, 75), (0.5, 80), (1, 80), (1, 85), (1.5, 85), (1.5, 95), (2, 90), (3, 100) and (4, 90).
Plot these points on a graph paper.
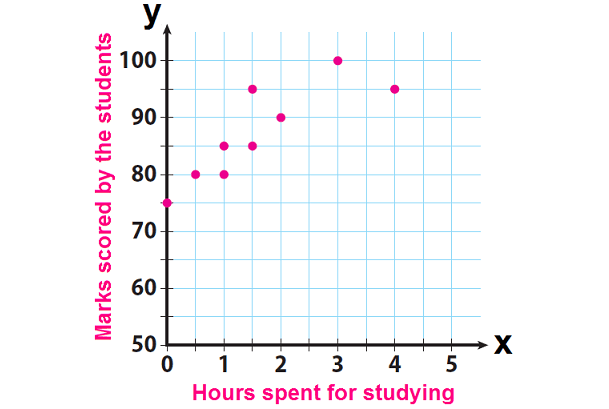
The graph shows a general upward trend. So the association between number of hours spent for studying and marks scored is positive. That is, as number of hours is getting increased, the marks scored is also getting increased.
Question 2 :
What trend can we see in the data given in question 1 ?
Answer :
In general, when students increase the number of study hours, the marks scored by them are also getting increased.
Question 3 :
Can we conclude the grade associated with studying for 10 hours would follow the trend in question 2 ?
Answer :
No
The graph shows a general upward trend, but the marks scored by the students cannot exceed 100.
Question 4 :
Can we say the relationship given in question 1 as positive or negative ?
Answer :
Yes, it is positive
Because, when one variable (x) is increased, the other variable (y) is also getting increased.
Question 5 :
The scatter plot shows David’s height at various ages. Describe the type of association between David’s age and his height. Explain.
Answer :
As David is getting older, his height increases roughly along a straight line on the graph, so the association is positive and basically linear.
Question 6 :
Alexa is training for a 10K race. For each of her training runs, she recorded the distance she ran and the time she ran. She made a scatter plot of her data and drew a trend line. Use the trend line to predict how long it would take Alexa to run 4.5 miles.
Answer :
For a distance of 4.5 miles, the trend line shows a time of 45 minutes. So, it will take Alexa about 45 minutes to run 4.5 miles.
Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
You can also visit the following web pages on different stuff in math.
WORD PROBLEMS
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Trigonometry word problems
Markup and markdown word problems
Word problems on mixed fractrions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Word problems on sets and venn diagrams
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Time, speed and distance shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the word problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by 7
Sum of all three digit numbers divisible by 8
Sum of all three digit numbers formed using 1, 3, 4
Sum of all three four digit numbers formed with non zero digits
Recent Articles
-
Write Equations for Proportional Relationships From Tables
Jun 02, 20 09:33 AM
Write Equations for Proportional Relationships From Tables
-
Graphing Proportional Relationships Worksheet
Jun 02, 20 02:58 AM
Graphing Proportional Relationships Worksheet
-
Graphing Proportional Relationships
Jun 02, 20 02:55 AM
Graphing Proportional Relationships - Examples with step by step explanation
