LOGISTIC FUNCTIONS AND THEIR GRAPHS

What is logistic function ?

Let a, b, c and k be positive constants, with b > 1.

A logistic growth function in x is a function that can be written in the form 

f(x)  =  c / (1 + a⋅b^x)   (or)  f(x)  =  c / (1 + a⋅e^-kx)

where the constant c is the limit of growth.

If b > 1 or k < 0, these formulas yield logistic decay functions.

By setting a  =  c  =  k  =  1, we obtain logistic function.

f(x)  =  1/(1 + e^-x)

This function, though related to exponential function e^x, cannot obtained from e^x by translation, reflection and vertical stretches and shrinks. 

Graph of Logistic Function

f(x)  =  1/(1 + e^-x)

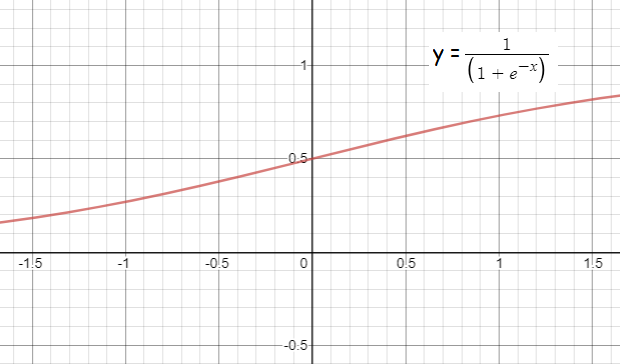
Domain :

Set of all real values.

Range :

(0, 1)

• The function is continuous and increasing for values of x.
• Symmetric about (0, 1/2), but neither even or odd.
• It is bounded below and above.
• There is no maximum and minimum.

Horizontal asymptotes :

y  =  0 and y  =  1

• There is no vertical asymptotes.

End behavior :

lim x-> -∞ f(x)  =  0 and  x-> ∞ f(x)  =  1

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.