LOGARITHM

Logarithm of a number to a given base is the index or the power to which the base must be raised to produce the number. That is, to make it equal to the given number.

Let us consider the three quantities, sat a, x and n and they can be related as follows.

If a^x = n, where n > 0, a > 0 and a ≠ 1, then x is said to be the logarithm of the number n to the base 'a',  symbolically it can be expressed as follows.

log_an = x

Here, 'n' is called argument.

Fundamental Laws of Logarithm

Law 1 :

Logarithm of product of two numbers is equal to the sum of the logarithms of the numbers to the same base.

log_amn = log_am + log_an

Law 2 :

Logarithm of the quotient of two numbers is equal to the difference of their logarithms to the same base.

log_a(m/n) = log_am - log_an

Law 3 :

Logarithm of a number raised to a power is equal to the power multiplied by the logarithm of the number to the same base.

log_amⁿ = nlog_am

Relationship between Exponents and Logarithms

Example 1 :

If log_am  =  x, then

m = a^x

Example 2 :

If k  =  x^y, then

log_xk = y

Multiplication of Logarithms

Multiplication of two or more logarithms can be simplified, if one of the following two conditions is met.

Condition (i) :

The argument of the first logarithm and the base of the second logarithm must be same.

Condition (ii) :

The base of the first logarithm and the argument of the second logarithm must be same.

Let us see how the multiplication of two logarithms can be simplified in the following examples.

Example 1 :

Simplify : log_ab ⋅ log_bc

In the above two logarithms, the argument of the first logarithm and the base of the second logarithm are same. 

So, we can simplify the multiplication of above two logarithms by removing the part circled in red color. 

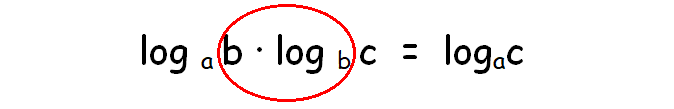
Example 2 :

Simplify : log_xy ⋅ log_zx

In the above two logarithms, the base of the first logarithm and the argument of the second logarithm are same.

So, we can simplify the multiplication of above two logarithms by removing the part marked in red color.

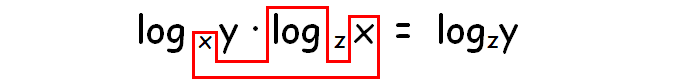
Change of Base

If the logarithm of a number to any base is given, then the logarithm of the same number to any other base can be determined from the following relation.

log_ba = log_xa ⋅ log_bx

log_ba = log_xa / log_xb

More clearly,

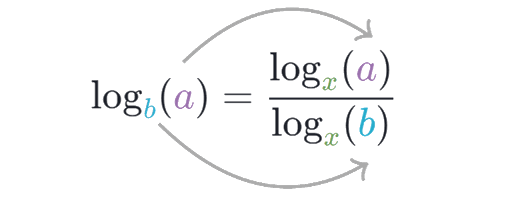
In the above example, the base of the given logarithm 'b' is changed to 'x'.

In this way, we can change the base of the given logarithm to any other base.

Inverse Properties of Logarithms

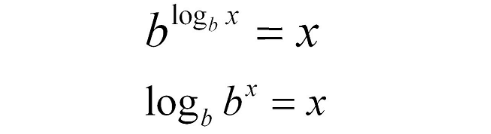
Some other Properties of Logarithms

Property 1 :

If you switch a logarithm from numerator to denominator or denominator to numerator, we have to interchange the argument and base.

Examples :

log_ab = 1/log_ba

5/(2log_xy) = 5log_yx/2

Property 2 :

Logarithm of any number to the same base is equal to 1.

Examples :

log_xx = 1

log₃3 = 1

The above property will not work, if both the base and argument are 1.

log₁1 ≠ 1

The reason for the above result is explained in the next property.

Property 3 :

Logarithm of 1 to any base is equal to 0.

Examples :

log_x1 = 0

log₃1 = 0

Notes

1. If the base is not given in a logarithm, it can be taken as 10.

log 10 = log₁₀ 10 = 1

log 1 = log₁₀ 1 = 0

2. Logarithm using base 10 is called Common logarithm and logarithm using base 'e' is called Natural logarithm.

Here, e ≈ 2.718 called exponential number.

Solved Problems

Problem 1 :

Find the logarithm of 125 to the base 5.

Solution :

Write 125 as a power of 5.

125 = 5 x 5 x 5

= 5³

log₅125 = log₅(5)³

= 3log₅5

= 3(1)

= 3

Problem 2 :

Find the logarithm 1728 to the base 2√3.

Solution :

Write 1728 as a power of 2√3.

1728 = 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3 x 3

1728 = 2⁶ x 3³

1728 = 2⁶ x [(√3)²]³

1728 = 2⁶ x (√3)⁶

1728 = (2√3)⁶

log_2√3(1728) = log_2√3(2√3)⁶

Using the power rule of logarithms,

= 6log_2√3(2√3)

= 6(1)

= 6

Problem 3 :

Find the logarithm of 0.001 to the base 0.1.

Solution :

log_0.10.001 = log_0.1(0.1)³

= 3log_0.10.1

= 3(1)

= 3

Problem 4 :

Find the logarithm 1/64 to the base 4.

Solution :

log₄(1/64) = log₄1 - log₄64

= 0 - log₄(4)³

= -3log₄4

= -3(1)

= -3

Problem 5 :

Find the logarithm of 0.3333...... to the base 3.

Solution :

log₃(0.3333......) = log₃(1/3)

= log₃1 - log₃3

= 0 - 1

= -1

Problem 6 :

If log_y(√2) = 1/4, find the value of y.

Write the equation in exponential form.

√2 = y^1/4

Raise to the power 4 on both sides.

(√2)⁴ = (y^1/4)⁴

(2^1/2)⁴ = y

2² = y

4 = y

Problem 7 :

Simplify :

(1/2)log₁₀25 - 2log₁₀3 + log₁₀18

Solution :

= (1/2)log₁₀25 - 2log₁₀3 + log₁₀18

Using power rule of logarithms,

= log₁₀25^1/2 - log₁₀3² + log₁₀18

= log₁₀(5²)^1/2 - log₁₀3² + log₁₀18

= log₁₀5 - log₁₀9 + log₁₀18

= log₁₀5 + log₁₀18 - log₁₀9

Using the product rule of logarithms,

= log₁₀(5 x 18) - log₁₀9

= log₁₀90 - log₁₀9

Using the quotient rule of logarithms,

= log₁₀(90/9)

= log₁₀10

= 1

Problem 8 :

What is the value of log₁ 1?

A)  log₁ 1 = 1

B)  log₁ 1 = 0

C)  log₁ 1 = Not Defined

Solution :

Video Lessons

Problem - 1

Problem - 2

Problem - 3

Problem - 4

Problem - 5

Problem - 6

Problem - 7

Problem - 8

Problem - 9

Problem - 10

Problem - 11

Problem - 12

Problem - 13

Problem - 14

Problem - 15

Problem - 16

Problem - 17

Problem - 18

Problem - 19

Problem - 20

Problem - 21

Problem - 22

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.