LOCUS OF A POINT EXAMPLES

Question 1 :

If R is any point on the x-axis and Q is any point on the y-axis and P is a variable point on RQ with RP = b, PQ = a. then find the equation of locus of P.

Solution :

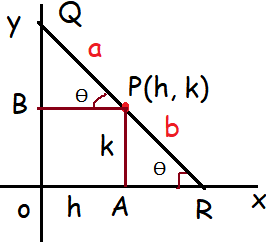
QR  =  a + b

sin²θ + cos²θ  = (k/b)² + (h/a)²

1  =  (k²/b²) + (h²/a²)

(h²/a²) + (k²/b²)  =  1

Question 2 :

If the points P(6, 2) and Q(−2, 1) and R are the vertices of a ΔPQR and R is the point on the locus y = x² − 3x + 4, then find the equation of the locus of centroid of ΔPQR

Solution :

Let R (a, b) 

Centroid of the triangle PQR be (h, k)

P(6, 2) Q(-2, 1) R(a, b)

Centroid of the triangle  =  (x₁+x₂+x₃)/3, (y₁+y₂+y₃)/3

(h, k)  =  (6-2+a)/3, (2+1+b)/3

(h, k)  =  (4+a)/3, (3+b)/3

Since the point (a, b) lies on the curve y = x² − 3x + 4

b = a² − 3a + 4

3k - 3  =  (3h - 4)² − 3(3h - 4) + 4

3k - 3  =  9h² + 16 + 24h + 9h + 12 + 4

9h² + 33h - 3k + 32 + 3  =  0

9h² + 33h - 3k + 35  =  0

Question 3 :

If Q is a point on the locus of x² + y² + 4x − 3y + 7 = 0, then find the equation of locus of P which divides segment OQ externally in the ratio 3:4, where O is origin.

Solution :

Let Q be (a, b) and P (h, k)

P is the point which divides the line segment joining the point OQ externally in the ratio 3 : 4

O (0, 0) Q (a, b)

  =  (mx₂ - mx₁)/(m - n), (my₂ - my₁)/(m - n)

  =  (3a - 0)/(3-4), (3b - 0)/(3-4)

 (h, k)  =  (-3a, -3b)

Q is a point on the locus of x² + y² + 4x − 3y + 7 = 0

a² + b² + 4a − 3b + 7 = 0

By applying the values of "a" and "b" in the above equation, we get

(-h/3)² + (-k/3)² + 4(-h/3) - 3(-k/3) + 7 = 0

(h²/9) + (k²/9) - (4h/3) + k + 7  =  0

h²+ k² - 12h + 9k + 63  =  0

Here h = x and k = y

x²+ y² - 12x + 9y + 63  =  0

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.