LINES AND ANGLES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
In this section, we are going to study about relationship between lines, parallel postulate, perpendicular postulate and angles formed by transversals.
Relationship between Lines
Two lines are parallel lines, if they are coplanar and do not intersect. Lines that do not intersect and are not coplanar are called skew lines. Similarly, two planes that do not intersect are called parallel planes.
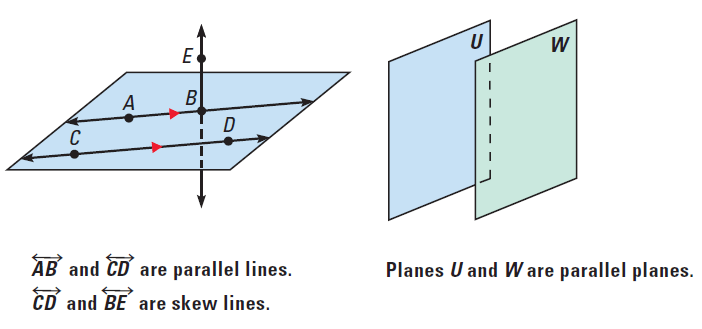
To write 'AB' is parallel to 'CD', we write AB||CD. Triangles like those AB and CD are used on diagrams to indicate that lines are parallel. Segments and rays are parallel if they lie on parallel lines.
For example, AB||CD.
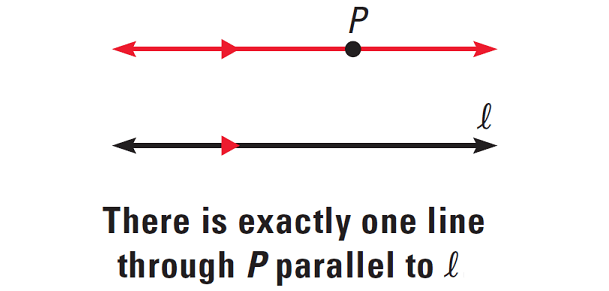
Parallel Postulate
If there is a line and a point not on the line, then there is exactly one line through the point parallel to the given line.
The diagram given below illustrates this.
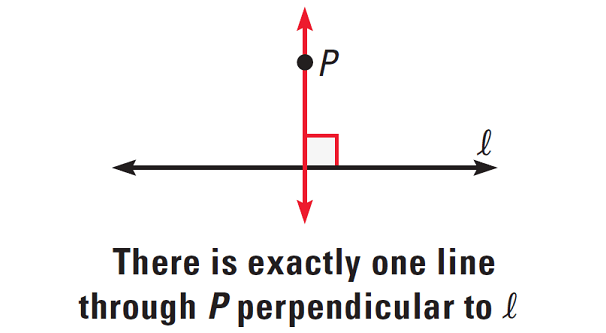
Perpendicular Postulate
If there is a line and a point not on the line, then there is exactly one line through the point perpendicular to the given line.
The diagram given below illustrates this.
Identifying Angles Formed by Transversals
A transversal is a line that intersects two or more coplanar lines at different points. For instance, in the diagrams below, line "t" is transversal. The angles formed by two lines and a transversal are given special names.
Corresponding Angles :
Two angles are corresponding angles, if they occupy corresponding positions.
For example, in the diagram given below, angles 1 and 5 are corresponding angles.
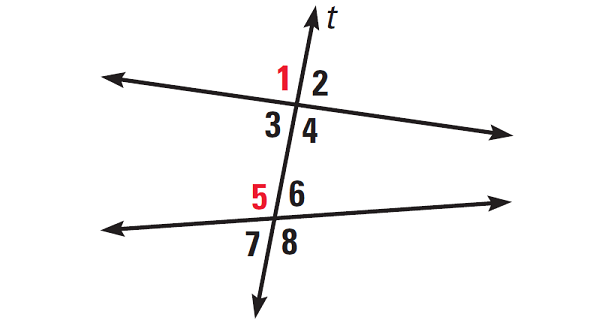
Alternate Exterior Angles :
Two angles are alternate exterior angles, if they lie outside the two lines on opposite sides of the transversal.
For example, in the diagram given below, angles 1 and 8 are alternate exterior angles.
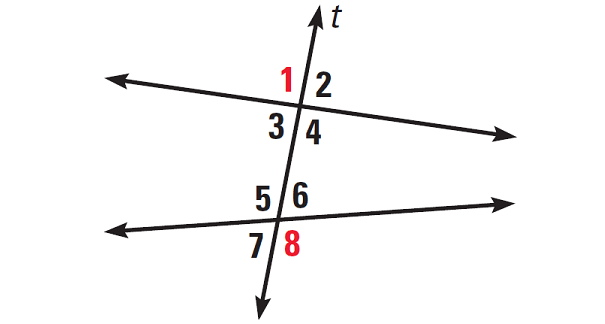
Alternate Interior Angles :
Two angles are alternate interior angles, if they lie between the two lines on opposite sides of the transversal.
For example, in the diagram given below, angles 3 and 6 are alternate interior angles.
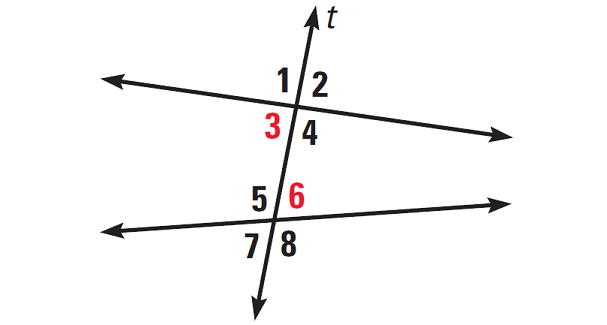
Consecutive Interior Angles :
Two angles are consecutive interior angles, if they lie between the two lines on the same side of the transversal.
Consecutive interior angles are also called same side interior angles.
For example, in the diagram given below, angles 3 and 5 are consecutive interior angles.
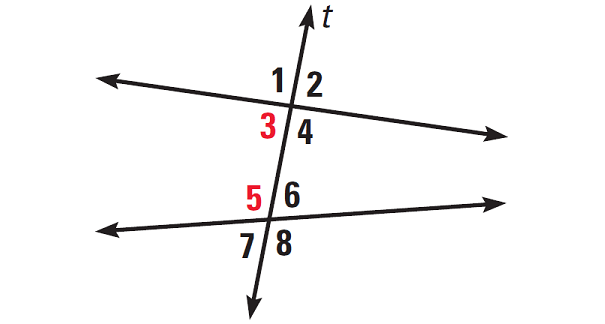
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4)
