LINEAR INEQUALITY WORD PROBLEMS

Problem 1 :

A and B are working on similar jobs, but their annual salaries differ by more than $6000. If the annual salary of A is more than B and B earns $27000 per year, then what are the possible values for the annual salary of A?

Solution :

Let x be the annual salary of A.

Given : The annual salaries of A and B differ by more than $6000.

x - 27000  >  6000

Add 27000 to each side. 

x  >  33000

So, the annual salary of A must be greater than $33000.

Problem 2 :

A worker can be paid according to the following schemes : In the first scheme he will be paid $500 plus $70 per hour, and in the second scheme he will paid $120 per hour. If he works for x hours, then for what value of x does the first scheme gives better wages?

Solution :

Let x be the number of working hours.

Amount of money, he gets in the first scheme :

=  500 + 70x -----(1)

Amount of money, he gets in the second scheme :

=  120x -----(2)

If the first scheme gives better wages, then we have

(1)  >  (2)

500 + 70x  >  120x

Subtract 70x from each side.

500  >  50x

Divide each side by 50.

10  >  x

x  <  10

When he works for less than 10 hours (x < 10), the first scheme gives better wages.

Problem 3 :

Find all pairs of consecutive odd natural numbers both of which are larger than 10 and their sum is less than 40.

Solution :

Let x and (x + 2) be the two required consecutive odd numbers.

Given : The sum of the numbers is 40.

x + (x + 2)  <  40

2x + 2  <  40

Subtract 2 from each side. 

 2x  <  38

x  <  19

Given : The numbers are greater than 10. 

So, the required two consecutive odd numbers must be greater than 10 and less than 19.

Therefore, the possible pairs of two consecutive odd numbers are

(11, 13), (13, 15) and (15, 17)

Problem 4 : 

A model rocket is launched from the ground. The height h reached by the rocket after t seconds from lift off is given by h(t) = -5t² + 100t, 0 ≤ t ≤ 20. If t is an integer, at what time the rocket is 495 feet above the ground ?

Solution :

According to the question, we have to find the value of t, when

h(t)  >  495 feet

- 5t² + 100t  >  495

Subtract 495 from each side. 

- 5t² + 100t - 495  >  0

Divide each side by (-5).

t² - 20t + 99  >  0

Solve the above quadratic inequality by factoring. 

t² - 11t - 9t + 99  >  0

t(t - 11) - 9(t - 11)  >  0

(t - 11)(t - 9)  >  0

If we assume (t - 11)(t - 9)  =  0, we will get the following values for t.    

Mark the values 9 and 11 on the number. 

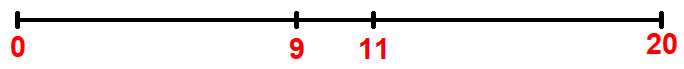
From the number line above, we can get the following three intervals.

(0, 9), (9, 11) and (11, 20)

When t ∊ (0, 9),

h(t)  <  495

When t ∊ (9, 11),

h(t)  >  495

When t ∊ (11, 20),

h(t)  <  495

We get h(t) > 495, when t ∊ (9, 11). Because t is an integer, the possible value we have for t in the interval is 10.

So, the rocket is 495 feet above the ground, after 10 seconds, it is launched from the ground.  

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.