LINEAR INEQUALITIES WORD PROBLEMS

Example 1 :

In 2010 Sacramento, California, received 23 inches in annual precipitation. In 2011, the city received 17 inches in annual precipitation. In which year was there more precipitation ?

Solution :

Locate the two integers 23 and 17 on a number line and mark them.

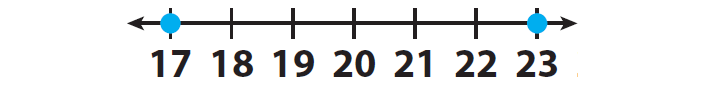
23 is to the right of 17 on the number line.

This means that 23 is greater than 17.

We can write the above situation in terms of inequality as

23 > 17

17 is to the left of 23 on the number line.

This means that 17 is less than 23.

We can write the above situation in terms of inequality as

17 < 23

So, there was more precipitation in 2010.

Example 2 :

An employer recruits experienced (x) and fresh workmen (y) for his firm under the condition that he cannot employ more then 9 people. Find the inequality which can relate x and y. 

Solution :

Given : x and y stand for number of experienced person and fresh workmen respectively. 

Total number of people recruited  is

=  x + y 

As per the question, total number of people (experienced + fresh) recruited should not be more than 9. 

That is, total number of people (x + y) recruited should be equal to 9 or less than 9. 

That is

x + y  ≤  9

Example 3 :

On the average experienced person does 5 units of work while a fresh one (y) does 3 units of work daily. But the employer has to maintain an output of at least 30 units of work per day. This situation can be expressed as 

Solution :

Given : x and y stand for number of experienced person and fresh workmen respectively. 

Total number of units of work done by experienced person per day is  5x. 

Total number of units of work done by fresh one per day is 3y. 

Total number of units of work done by both experienced person and fresh one per day is 

=  5x + 3y

As per the question, total number of units of work per day should be at least 30 units. 

That is, total number of units of work (5x + 3y) should be equal to 30 or more than 30. 

So, this situation can be expressed as

5x + 3y  ≥  30

Example 4 :

The rules and regulations demand that the employer should employ not more than 5 experienced hands (x) to 1 fresh one (y). How can this fact be expressed ? 

Solution :

Given : x and y stand for number of experienced person and fresh workmen respectively. 

As per the question, no. of experienced hands(x) should not be more than 5 

That is, no. of experienced hands should be equal to 5 or less than 5 

So, we have

x  ≤  5    or    x/5  ≤  1 -----(1)

According to the question, no. of fresh hands is equal to 1. 

So, we have

y  =  1

Substitute y for z in (1). 

(1)-----> x/5  ≤  y

Multiply each side by 5.

x  ≤  5y    (or)    5y  ≥  x

So, the situation can be expressed as 

x  ≤  5y    (or)    5y  ≥  x

Example 5 :

The union however forbids the employer to employ less than 2 experienced persons (x) to each fresh person (y). How can this situation be expressed ? 

Solution :

Given : x and y stand for number of experienced person and fresh workmen respectively. 

In this problem, the word "forbid" plays an important role. 

Meaning of "Forbid" is "Not allowed" 

The union forbids the employer to employ less than 2 experienced hands.

That is, the union does not allow the employer to employ less than 2 experienced hands. 

Therefore, the employer should employ 2 or more than 2 experienced hands. 

Then, we have

x  ≥  2

x/2  ≥  1 -----(1)

And also, no. of fresh persons to be employed is equal to 1 

Then, we have

y  =  1

Substitute y for 1 in (1).

(1)-----> x/2  ≥  y     (or)    y  ≤  x/2

So, the situation can be expressed as 

x/2  ≥  y     (or)    y  ≤  x/2

Example 6 :

A company produces two products A and B, each of which requires processing in two machines. The first machine can be used at most for 60 hours, the second machine can be used at most for 40 hours. The product A requires 2 hours on machine one and one hour on machine two. The product B requires one hour on machine one and two hours on machine two. Express above situation using linear inequalities.

Solution :

In this question, we have two quantities - products and hours.

You may get confused to assign variable for which quantity.

Look at the quantity for which the minimum or maximum value is given. Don't assign variable for the quantity for which you have minimum or maximum value. Assign variable for the other quantity.

In this question, since the maximum value is given for number of hours, don't assign variable for number of hours. Assign variable for the other quantity, that is products.

Let x and y be the number of units of products A and B respectively.

Number of units can never be a negative value.

So, x ≥ 0 and y ≥ 0.

To understand the question better, we can represent the given information in a table as shown below.

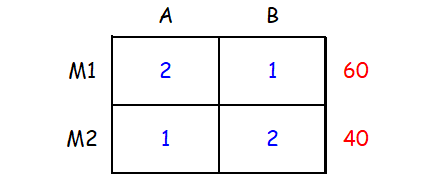
From the first and second rows of the table,

2x + y ≤ 60

x + 2y ≤ 40

And also, x ≥ 0 and y ≥ 0.

Example 7 :

Two machines (I and II) produce two grades of plywood, grade A and grade B. In one hour of operation machine I produces two units of grade A and one unit of grade B, while machine II, in one hour of operation produces three units of grade A and four units of grade B. The machines are required to meet a production schedule of at least fourteen units of grade A and twelve units of grade B. Express this using linear inequalities and draw the graph.

Solution :

In this question, we have two quantities - grades of plywood and hours.

Since the minimum value is given for grades of plywood, don't assign variable for number of grades of plywood. Assign variable for the other quantity, that is number of hours.

Let x and y be the number of hours required on machines I and II respectively.

Number of hours can never be a negative value.

So, x ≥ 0 and y ≥ 0.

We can represent the given information in a table as shown below.

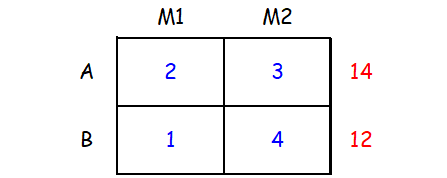
From the first and second rows of the table,

2x + 3y ≥ 14

x + 4y ≥ 12

And also, x ≥ 0 and y ≥ 0.

Example 8 :

A manufacturer produces two products A and B, and has his machines in operation for 24 hours a day. Production of A requires 2 hours of processing in machine M1 and 6 hours in machine M2. Production of B requires 6 hours of processing in machine M1 and 2 hours in machine M2. The manufacturer earns a profit of $5 on each unit of A and $2 on each unit of B. How many units of each product should be produced in a day in order to achieve maximum profit?

Solution :

Since we have to find the number of units of products A and B to achieve the maximum product, assign variables for the products.

Let x and y be the number of units of products A and B respectively.

Since the target is to achieve the maximum profit, we have to set up an objective function which results profit.

Let z be the total profit earned.

Profit for each unit of A = $5.

Profit for each unit of B = $2.

Then, we have

z = 5x + 2y

Now, we have to find the values of x and y for which z is maximum.

We can represent the given information in a table as shown below.

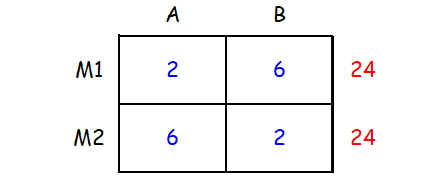
From the first and second rows of the table,

2x + 6y ≤ 24

6x + 2y ≤ 24

And also, x ≥ 0 and y ≥ 0.

To find the values of x and y for which z is maximum, we have to graph the above system of inequalities.

For graphing purpose, assume the inequalities as equation and do all possible simplification.

Graph the following system of equations

x + 3y = 12

3x + y = 12

and shade the feasible region which satisfy the following system of inequalities.

x + 3y ≤ 12

3x + y ≤ 12

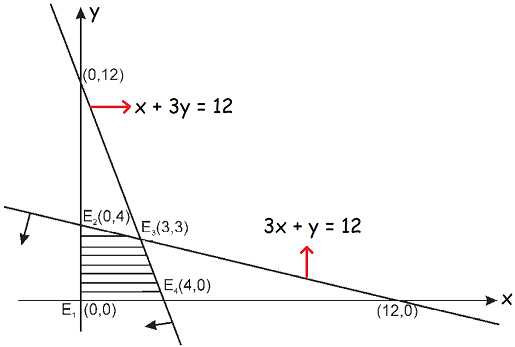
The boundary points of the feasible region or shaded region are

(0, 0), (4, 0), (3, 3) and (0, 4)

Find the value z in each of the above points.

(0, 0) ----> z = 5(0) + 2(0) = 0 + 0 = 0

(4, 0) ----> z = 5(4) + 2(0) = 20 + 0 = 20

(3, 3) ----> z = 5(3) + 2(3) = 15 + 6 = 21

(0, 4) ----> z = 5(0) + 2(4) = 0 + 8 = 8

In the above four values of z, the maximum value is 21 at the point (3, 3).

(3, 3) ----> x = 3 and y = 3.

Thus, to achieve maximum profit the manufacturer should produce 3 units each of both the products A and B.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.