Linear Inequalities in One Variable

LINEAR INEQUALITIES IN ONE VARIABLE

Solving a linear inequality in one variable is similar to solving a linear equation in one variable.

We can use the following properties of equality to solve a linear inequaltiy in one variable.

1. Addition property of equality

2. Subtraction Property of equality

3. Multiplication property of equality

4. Division property of equality

Important Note :

When you multiply or divide both sides of an inequality by the same negative number, you have to slip the inequality sign.

For example, if an inequality contains less than, it has to be changed to greater than.

Video Lesson

Solved Examples

Solve the each of following inequalities and graph the solution.

Example 1 :

2(x - 3) ≥ 3x – 4

Solution :

2(x - 3) ≥ 3x - 4

2x – 6 ≥ 3x – 4

Subtract 3x from both sides.

-x – 6 ≥ –4

Add 6 to both sides.

-x ≥ 2

Multiply both sides by -1.

x ≤ -2

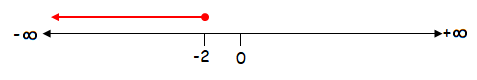
The solution of the given inequality is (-∞, -2].

Example 2 :

Solution :

The least common multiple of the denominators (3, 6) is 6. Multiply both sides of the inequality by 6 to get rid of the denominators 3 and 6.

2x + 4 < 5x - 6

Subtract 5x from both sides.

-3x + 4 < -6

Subtract 4 from both sides.

-3x < -10

Divide both sides by -3.

x > ¹⁰⁄₃

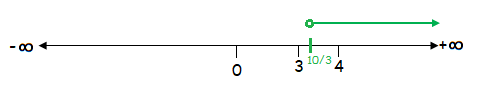
The solution of the given inequality is (¹⁰⁄₃, +∞).

Example 3 :

2(x + 2) ≤ x – 5

Solution :

2(x + 2) ≤ x – 5

2x + 4 ≤ x – 5

Subtract x from both sides.

x + 4 ≤ –5

Subtract 4 from both sides.

x ≤ –9

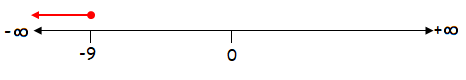
The solution of the given inequality is (-∞, -9].

Example 4 :

Solution :

12 ≥ 2y - 5 ≥ -6

Add 5 to each term.

17 ≥ 2y ≥ -1

Divide each term by 2.

17 ≥ 2y ≥ -1

¹⁷⁄₂ ≥ y ≥ -¹⁄₂

-½ ≤ y ≤ ¹⁷⁄₂

The solution of the given inequality is [¹⁷⁄₂, -½].

Example 5 :

0 ≤ 2z + 5 < 8

Solution :

0 ≤ 2z + 5 < 8

Subtract 5 from each term.

-5 ≤ 2z < 3

Divide each term by 2.

-⁵⁄₂ ≤ z < ³⁄₂

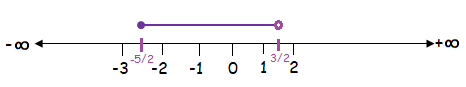
The solution of the given inequality is [-⁵⁄₂, ³⁄₂).

Example 6 :

Solution :

The least common multiple of the denominators (4, 3) is 12. Multiply both sides of the inequality by 12 to get rid of the denominators 4 and 3.

3(x - 5) + 4(3 - 2x) < -24

3x - 15 + 12 - 8x < -24

-5x - 3 < -24

Add 3 to both sides.

-5x < -21

Divide both sides by -5.

x > ²¹⁄₅

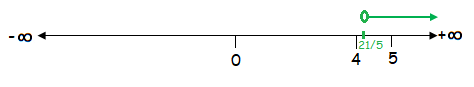
The solution of the given inequality is (²¹⁄₅, +∞).

Example 7 :

Solution :

The least common multiple of the denominators (2, 5) is 10. Multiply both sides of the inequality by 10 to get rid of the denominators 2 and 5.

5(2y – 3) + 2(3y – 1) < 10y – 10

10y - 15 + 6y - 2 < 10y - 10

16y – 17 < 10y – 10

Subtract 10y from both sides.

6y - 17 < -10

Add 17 to both sides.

6y < 7

Divide both sides by 6.

y < ⁷⁄₆

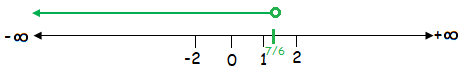
The solution of the given inequality is (-∞, ⁷⁄₆).

Example 8 :

Solution :

Ther least common multiple of the denominators (6, 8) is 24. Multiply both sides of the inequality by 24 to get rid of the denominators 6 and 8.

4(3 - 4y) - 3(2y - 3) ≥ 48 - 24y

12 - 16y - 6y + 9 ≥ 48 - 24y

-22y + 21 ≥ 48 - 24y

Add 24y to both sides.

2y + 21 ≥ 48

Subtract 21 from both sides.

2y ≥ 27

Divide both sides by 2.

y ≥ ²⁷⁄₂

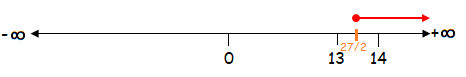
The solution of the given inequality is [²⁷⁄₂, +∞).

Example 9 :

Solution :

x - 4 - 4x ≤ 30 - 10x

-3x - 4 ≤ 30 - 10x

Add 10x to both sides.

7x - 4 ≤ 30

Add 4 to both sides.

7x ≤ 34

Divide both sides by 7.

x ≤ ³⁴⁄₇

The solution of the given inequality is (-∞, ³⁴⁄₇].

Example 10 :

Solution :

4 > 3y – 1 > -4

Add 1 to each term.

5 > 3y > -3

Divided each term by 3.

⁵⁄₃ > y > -1

-1 < y < ⁵⁄₃

The solution of the given inequality is (-1, ⁵⁄₃)

Example 11 :

-6 < 5t – 1 < 0

Solution :

-6 < 5t – 1 < 0

Add 1 to each term.

-5 < 5t < 1

Divide each term by 5.

-1 < t < ⅕

The solution of the given inequality is (-1, 1/5)

Example 12 :

Solution :

3(3 - x) + 2(5x - 2) < -6

9 - 3x + 10x - 4 < -6

7x + 5 < -6

Subtract 5 from both sides.

7x < -11

Divide botgh sides by 7.

x < -¹¹⁄₇

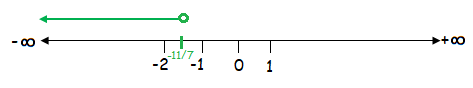
The solution of the given inequality is (-∞, -¹¹⁄₇).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.