LINEAR INEQUALITIES AND GRAPHS WORKSHEET 

Problem 1 :

The sum of 120k and 215j does not exceed 2,500.

Which of the following inequalities represents the statement above?

(A)  120k + 215j < 2500

(B)  120k + 215j > 2500

(C)  120k + 215j ≤ 2500

(D)  120k + 215j ≥ 2500

Problem 2 :

One half of a number decreased by 3 is at most -5.

Which of the following inequalities represents the statement above?

(A)  ½x - 3 ≤ -5

(B)  3 - ½x ≤ -5

(C)  ½x - 3 < -5

(D)  3 -  ½x < -5

Problem 3 :

Which of the following numbers is NOT a solution to the inequality

(A)  0

(B)  1

(C)  2

(D)  3

Problem 4 :

0.6(k - 7) - 0.3k > 1.8 + 0.9k

Which of the following inequalities is equivalent to the inequality above?

(A)  k < 10

(B)  k < -10

(C)  k > 10

(D)  k > -10

Problem 5 :

4m - 3 ≤ 2(m + 1)  or  7m + 25 < 15 + 9m

Which of the following numbers is a solution to the compound inequality above?

(A)  2

(B)  3

(C)  4

(D)  5

Problem 6 :

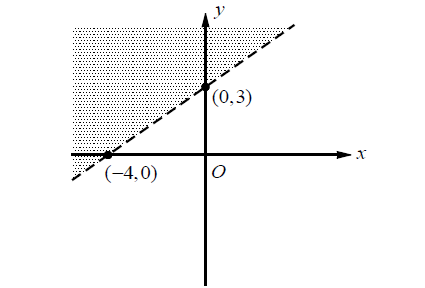
Which of the following inequalities represents the graph above?

(A)  4y - 3x > 12

(B)  4y - 3x < 12

(C)  3y - 4x > 12

(D)  3y - 4x < 12

Problem 7 :

2y - 3x ≤ 6

y > 1 - x

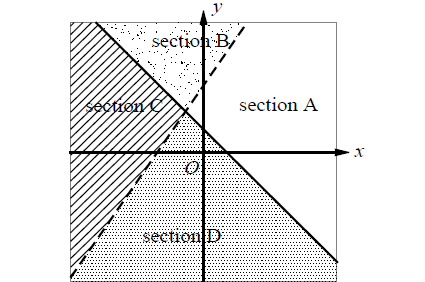
A system of inequalities and a graph are shown above. Which section or sections of the graph could represent all of the solutions to the system?

(A)  Section A

(B)  Section B

(C)  Section C

(D)  Section D

Problem 8 :

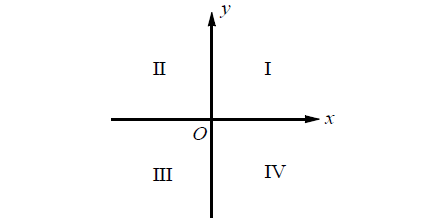
If the system of inequalities 3 ≥ x and -1 ≤ y is graphed in the xy-plane above, which quadrant contains no solution to the system?

(A)  Quadrant II

(B)  Quadrant III

(C)  Quadrant IV

(D)  All the four quadrants contain solutions.

Problem 9 :

y < ax + 1

y > bx - 1

In the xy-plane, if (1, 0) is a solution to the system of inequalities above, which of the following must be true?

I.  a > -1

II.  a + b > 0

III.  b < 1

(A)  I only

(B)  I and II only

(C)  I and III only

(D)  I, II, and III

Problem 10 :

y ≥ 12x + 600

y ≥ -6x + 330

In the xy-plane, if (x, y) lies in the solution set of the system of inequalities above, what is the minimum possible value of y?

Problem 11 :

-6 ≤ 3 - 2x ≤ 9

In the compound inequality above, find the greatest possible value of (x - 1).

Problem 12 :

4x - 2 > 17  and  3x + 5 < 24

Solve the above system of inequalities for integer value of x.

1. Answer :

120k + 215j ≤ 2500

Therefore, the correct answer is option (C).

2. Answer :

Let x be the number.

½x - 3 ≤ -5

Therefore, the correct answer is option (A).

3. Answer :

b ≤ 2.2

In the given answer choices, 3 is not a solution.

Therefore, the correct answer is option (D).

4. Answer :

0.6(k - 7) - 0.3k > 1.8 + 0.9k

0.6k - 4.2 - 0.3k > 1.8 + 0.9k

0.3k - 4.2 > 1.8 + 0.9k

-0.6k - 4.2 > 1.8

-0.6k > 6

k < -10

Therefore, the correct answer is option (B).

5. Answer :

4m - 3 ≤ 2(m + 1)  or  7m + 23 < 15 + 9m

m ≤ 2.5  or  m > 5

Among the answer choices, 2 is the only solution to the compound inequality.

Therefore, the correct answer is option (A).

6. Answer :

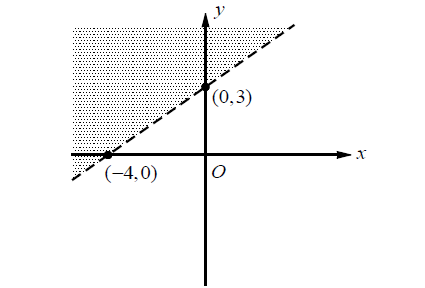
In the above graph, rise of the boundary line is 3 and run is 4.

slope m = ¾

y-intercept of the boundary line is 3.

Equation of the boundary line in slope-intercept form :

y = (¾)x + 3

Write the above equation in standard form.

4y = 3x + 12

4y - 3x = 12

Conparing the above equation with the given answer choices, options (C) and (D) can be rejected.

Select a point in the shaded region and check with the inequalities in options (A) and (B). Let's use (-4, 3).

In option (A),

4y - 3x > 12

4(-4) - 3(3) > 12

-16 - 9 > 12

-25 > 12

(false)

In option (B),

4y - 3x < 12

4(-4) - 3(3) < 12

-16 - 9 < 12

-25 < 12

(true)

Therefore, the correct answer is option (B).

7. Answer :

Select a random point in each section and check the given system of inequalities.

Let's use (3, 0) in section A.

2y - 3x ≤ 6 ----> -9 ≤ 6 (true)

y > 1 - x ----> 0 > -2 (true)

Since the point in section A satisfies both the inequalities in the given system, we dont have to verify the other sections.

Therefore, the correct answer is option (A).

8. Answer :

3 ≥ x

-1 ≤ y

Graph the given system of inequalities in the xy-plane.

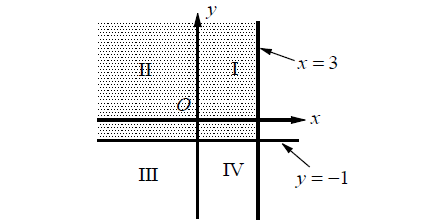
The solution to the system of inequalities is the shaded region shown in the graph above. Its solutions include points in all four quadrants.

Therefore, the correct answer is option (D).

9. Answer :

y < ax + 1

y > bx - 1

Since (1, 0) is a solution to the system of inequalities, substitute x = 1 and y = 0 in the given inequalities.

y < ax + 1 :

0 < a(1) + 1

0 < a + 1

-1 < a

a > -1

Statement I is true.

y < bx - 1 :

0 > b(1) - 1

0 > b - 1

1 > b

b < 1

Statement III is true.

Since a > -1, the possible values for a are

a = 0, 1, 2, .......

Since b > 1, the possible values for b are

b = ....... -2, -1, 0

When a = 0 and b = -2,

a + b > 0 ----> -2 > 0 (false)

When a = 1 and b = -1,

a + b > 0 ----> 0 > 0 (false)

When a = 2 and b = 0,

a + b > 0 ----> 2 > 0 (true)

We for some set of values of a and b, statement III is false and for some set of values of a and b, statement III is true.

So, we can not conclude that statement III is true or false.

Therefore, the correct answer is option (C).

10. Answer :

y ≥ 12x + 600 ----(1)

y ≥ -6x + 330 ----(2)

Multiply both sides of (2) by 2 and add it to (1).

(1) + 2 ⋅ (2)

3y ≥ 1260

y ≥ 420

Therefore, the minimum possible value of y is 420.

10. Answer :

-6 ≤ 3 - 2x ≤ 9

-9 ≤ -2x ≤ 12

4.5 ≥ x ≥ -6

3.5 ≥ x - 1 ≥ -7

-7 ≤ x - 1 ≤ 3.5

Therefore, the greatest possible value of (x - 1) is 3.5.

10. Answer :

4x - 2 > 17  and  3x + 5 < 24

Combining the above two inequalities,

4.75 < x < 6.33

The integer value for x is 5 or 6.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.