LINEAR FUNCTIONS AND LINES

Slope :

Consider a line in the coordinate plane, along with two points (x₁,y₁) and (x₂,y₂) on the line. Draw two right triangles with horizontal and vertical edges as in the figure below. 

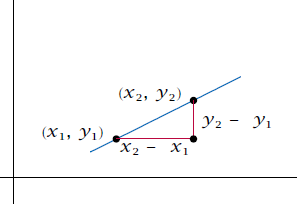
Thus the ratio (y₂−y₁) / (x₂−x₁) is a constant depending only on the line and not on the particular points (x₁,_y1) and (x₂,y₂) chosen on the line. This constant is called the slope of the line.

If (x₁,y₁) and (x_2,y₂) are any two points on a line, with x₁≠x2, then the slope of the line is

(y₂ − y₁) / (x₂ − x₁)

Methods of Finding Equation of a Line

The equation of a line, given its slope and one point on it :

The line in the xy-plane that has slope "m" and contains the point (x₁, y₁) is given by the equation

y − y₁ = m(x − x₁)

The equation of a line, given two points on it :

The line in the xy-plane that contains the points (x₁,y₁) and (x₂,y₂), where x1 ≠ x2, is given by the equation

(y − y₁) / (y₂ − y₁)  =  (x - x₁) / (x₂ − x₁)

The equation of a line, given its slope and vertical axis intersection :

The line in the xy-plane with slope m that intersects the y-axis at (0, b) is given by the equation

y = mx + b.

Linear functions :

A linear function is a function f of the form

f(x) = mx + b,

where m and b are constants

Constant functions :

A constant function is a function f of the form

f(x) = b,

where b is a constant.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.