LINEAR COST FUNCTION

This is the function where the cost curve of a particular product will be a straight line. 

Mostly this function is used to find the total cost of "x" units of the products produced.

For any product, if the cost curve is linear, the linear cost function of the product will be in the form of

y = Ax + B

The picture shown below clearly explains what each letter in the above linear cost function stands for.

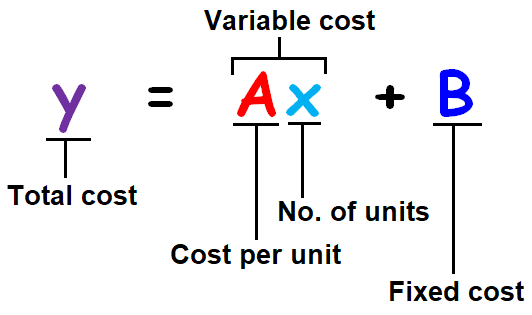
Linear cost function is called as bi parametric function. Here the two parameters are "A" and "B".

Once the two parameters "A" and "B" are known, the complete function can be known.

In co-ordinate geometry, the same linear cost function is called as slope intercept form equation of a straight line. 

Solving Word Problems Using Linear Cost Function

The following steps are involved in solving word problems on linear cost function.

Step 1 :

First we have to go through the question carefully and understand the information given in the question.

After having gone through the question, we have to conclude whether the information given in the question fits linear-cost function.

If the information fits the linear-cost function, we have to follow step 2

Step 2 :

Target :

We have to know what has to be found.

In linear-cost function, mostly the target would be to find either the value of 'y' (total cost) or 'x' (number of units). 

Step 3 :

In step 3,  we have to calculate the two constants "A"  and "B" from the information given in the questions. It has been shown clearly in the example problem given below. 

Step 4 :

Once the values of 'A' and 'B'  in   y = Ax + B are found, the linear-cost function would be completely known. 

Step 5 :

After step 4, based on the target of the question, we have to find either the value of 'y' or 'x' for the given input. 

For example, if the value of 'x' (number of units) is given, we can find the value of 'y' (total cost).

If the value of 'y' (total cost) is given, we can find the value of 'x' (number of units). 

Solving Word problem on Linear Cost Function

Problem :

A manufacturer produces 80 units of a particular product at a cost of $ 220000 and 125 units at a cost of $ 287500. Assuming the cost curve to be linear, find the cost of 95 units. 

Solution :

Step 1 :

When we go through the question, it is very clear that the cost curve is linear.

And the function which best fits the given information will be a linear-cost function.

That is,                              y  =  Ax + B

Here

y ----> Total cost

x ----> Number of units

Step 2 :

Target :

We have to find the value of 'y' for x = 95.

Step 3 :

From the question, we have

x  =  80     and     y = 220000

x  =  75     and     y = 287500

Step 4 :

When we substitute the above values of 'x' and 'y' in

y = Ax + B,

we get 

220000  =  80A + B

287500  =  75A + B

Step 5 :

When we solve the above two linear equations for A and B, we get  

A  =  1500   and   B  =  100000

Step 6 :

From A  =  1500 and B  =  100000, the linear-cost function for the given information is  

y  = 1500x  +  100000

Step 7 :

To estimate the value of 'y' for x = 95, we have to substitute 95 for x in

y  =  1500x + 100000

Then, 

y  =  1500x95 + 100000

y  =  142500  +  100000

y  =  242500

So, the cost of 95 units is $242500.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.