LENGTH OF ARC GRADE 11 WORD PROBLEMS

Problem 1 :

What must be the radius of a circular running path, around which an athlete must run 5 times in order to describe 1 km?

Solution :

Distance covered by athlete = 1 km 

5 ⋅ 2πr = 1 km 

5 ⋅ 2 ⋅ (3.14) ⋅ r = 1000 m

r = 31.84 m

Problem 2 :

In a circle of diameter 40 cm, a chord is of length 20 cm. Find the length of the minor arc of the chord.

Solution :

Let arc AB  =  s. 

It is given that OA  =  20 cm and chord AB  =  20 cm.

Hence triangle OAB is an equilateral triangle.

<AOB  =  60 degree (or) (π/3) radians

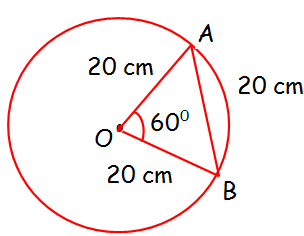
 θ = arc length/radius

(π/3)  =  s/20

s  =  20π/3

π  =  3.14

s  =  20(3.14)/3  =  20.93

So, the required arc length is 20.93 cm.

Problem 3 :

Find the degree measure of the angle subtended at the center of circle of radius 100 cm by an arc of length 22 cm.

Solution :

Radius of the circle  =  100 cm

Length of arc  =  22 cm

 θ = arc length/radius

  =  22/100

Radian measure  =  (π/180) Degreee measure

22/100  =  (22/7)/180 ⋅ Degree measure

Degree measure =  (22 ⋅ 7 ⋅ 180)/(22 ⋅ 100)

=  126/10

12^◦ (6/10)

Multiplying 6/10 by 60, we get 36'

So, the required angle is 12^◦ 36'

Problem 4 :

What is the length of the arc intercepted by a central angle of measure 41^◦ in a circle of radius 10 ft?

Solution :

arc length   =   (θ/360) ⋅ 2 ⋅ π ⋅ r

=  (41/360) ⋅ 2 ⋅ (3.14) ⋅ r

=  7.16 feet

So, the required arc length is 7.16 feet.

Problem 5 :

If in two circles, arcs of the same length subtend angles 60^◦ and 75^◦ at the center, find the ratio of their radii.

Solution :

Let r₁ and r₂ be the radii of the given circles and let their arcs of same length subtend angles of 60 degree and 75 degree at their centers.

(1)  =  (2)  

πr₁ /3  =  5πr₂ /12

r_1/r_{2  =}   (5π/π)(3/12)

r_1/r_2  =   5/4

r_{1 :} r₂  =  5 : 4

Problem 6 :

A circle has a radius of 6 inches. Find the length of the arc intercepted by a central angle of 45^◦ .

Solution :

Length of arc S = rθ

radius = 6 inches

θ = 45^◦

Here the angle is given as degree measure, to convert into radian measure, we have to multiply by π/180

= 45 x (π/180)

= π/4

Applying the radian measure in the formula, we get

S = 6(π/4)

= (6/4) π

= 1.5π inches

Problem 7 :

A circle has a radius of 5cm. Find the length of the arc intercepted by a central angle of 38^◦

Solution :

Length of arc S = rθ

radius = 5 cm

θ = 38^◦

Here the angle is given as degree measure, to convert into radian measure, we have to multiply by π/180

= 38 x (π/180)

= 38π/180

= 19π/90

Applying the radian measure in the formula, we get

S = 5(19π/90)

= (95/90) π

= 1.05 π inches

Problem 8 :

A circle has a radius of 10 ft. Find the length of the arc intercepted by a central angle of 5π/12

Solution :

Length of arc S = rθ

radius = 10 ft

θ = 5π/12

Applying these values in the formula, we get

S = 10(5π/12)

= 50π/12

= 4.16 π ft.

Problem 9 :

Find the degree measure to the nearest tenth of the central angle that has an arc length of 87 and a radius of 16 cm.

Solution :

Length of arc S = rθ

Length of arc S = 87

radius = 16 cm

θ = ? (in radian)

Applying these values in the formula, we get

87 = 16(θ)

θ = 87/16

Converting in to degree

= (87/16) x (180/π)

= 311.7

Approximately 312.

Problem 10 :

Find the degree measure to the nearest tenth of the central angle that has an arc length of 5.6 and a radius of 12 cm.

Solution :

Length of arc S = rθ

Length of arc S = 5.6

radius = 12 cm

θ = ? (in radian)

Applying these values in the formula, we get

5.6 = 12(θ)

θ = 5.6/12

Converting in to degree

= (5.6/12) x (180/π)

= 26.75

Approximately 26.75

Problem 11 :

A sector has arc length 12 cm and a central angle measuring 1.25 radians. Find the radius and the area of the sector.

Solution :

Length of arc S = rθ

Length of arc S = 12 cm

radius = ?

θ = 1.25 radians

Applying these values in the formula, we get

12 = r(1.25)

r = 12/1.25

r = 9.6 cm

Area of sector = (1/2)r² θ

= (1/2) (9.6)² (1.25)

= 57.6 cm²

Problem 12 :

Find the area of the sector of the circle that has a central angle measure of π/6 and a radius of 14 cm.

Solution :

radius = 14 cm

θ = π/6

Area of sector = (1/2)r² θ

= (1/2) (14)² (π/6)

= 16.3π cm²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.