LEAST COMMON MULTIPLE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Let us now write the multiples of 5 and 7.
Multiples of 5 are
5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70,…
Multiples of 7 are
7, 14, 21, 28, 35, 42, 49, 56, 63, 70,…
Here, the common multiples of 5 and 7 are 35 and 70 and will go on without ending.
As multiples of a number are infinite, we can think of the Least Common Multiple of numbers, shortly denoted as LCM.
Think about the following situations.
Situation 1 :
Write the multiplication table of 4 and 5 (up to 10).
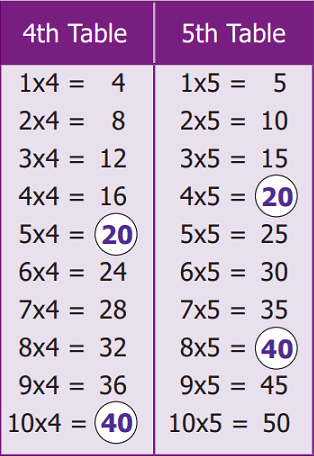
Observing the multiplication tables, can you find the multiples (product of numbers) that are the same in the 4th table and 5th table ?.
If yes, what are they?
Yes, they are 20, 40,…etc.
From the multiples of 4 and 5, we can easily find that 20 is the least common multiple of 4 and 5.
Situation 2 :
Consider the red and the blue colored floor mats of length 4 units and 5 units as follows.

Five red colored floor mats of 4 units each can be arranged as follows. Its total length is
5 x 4 = 20 units

Four blue colored floor mats of 5 units each can be arranged as follows. Its total length is also the same
4 x 5 = 20 units

Note that the 5 floor mats each of length 4 units are required to equal 4 floor mats each of length 5 units and that is, the length 20 units is the smallest common length that can be matched by both sizes.
From the above, it shows that the least common multiple of 4 and 5 is
4 x 5 = 20
The Least Common Multiple of any two non-zero whole numbers is the smallest or the lowest common multiple of both the numbers.
The Least Common Multiple of the numbers x and y can be written as LCM (x, y).
We can find the least common multiple of two or more numbers by the following methods.
1. Division Method
2. Prime factorization Method
(LCM ----> Least Common Multiple)
Example :
Find the LCM of 156 and 124.
Solution by Division Method :
Step 1 :
Start with the smallest prime factor and go on dividing till all the numbers are divided as shown below.
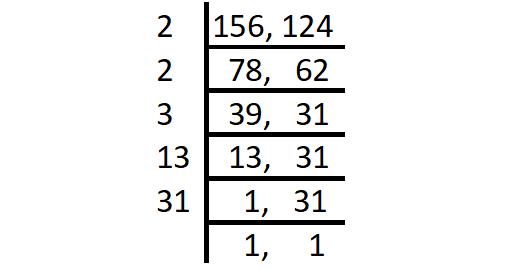
Step 2 :
LCM = Product of all prime factors
= 2 x 2 x 3 x 13 x 31
= 4836
Thus, the LCM of 156 and 124 is 4836.
Solution by Prime Factorization Method :
Step 1 :
Write the prime factors of 156 and 124 as shown below (use of divisibility test rules will also help).
156 = 2 x 2 x 3 x 13
124 = 2 x 2 x 31
Step 2 :
The prime factor 2 appears a maximum of 2 times in the prime factorization of 156 and 124.
The prime factors 3 and 13 appear only 1 time in the prime factorization of 156, the prime factor 31 appears only 1 time in the prime factorization of 124.
Hence, the required LCM is
= (2 x 2) x 3 x 13 x 31
= 4836
Solved Problems
Problem 1 :
Find the LCM of the following set of numbers using prime factorization method.
6, 9
Solution :
Step 1 :
Write the prime factors of 6 and 9 as shown below.
6 = 2 x 3
9 = 3 x 3
Step 2 :
The prime factor 3 appears a maximum of 2 times in the prime factorization of 9.
The prime factor 2 appears only 1 time in the prime factorization of 6.
Hence, the required LCM is
= (3 x 3) x 2
= 9 x 2
= 18
Problem 2 :
Find the LCM of the following set of numbers using prime factorization method.
8, 12
Solution :
Step 1 :
Write the prime factors of 8 and 12 as shown below.
8 = 2 x 2 x 2
12 = 2 x 2 x 3
Step 2 :
The prime factor 2 appears a maximum of 3 times in the prime factorization of 8.
The prime factor 3 appears only 1 time in the prime factorization of 12.
Hence, the required LCM is
= (2 x 2 x 2) x 3
= 8 x 3
= 24
Problem 3 :
Find the LCM of the following set of numbers using division method.
16, 24
Solution :
Step 1 :
Start with the smallest prime factor and go on dividing till all the numbers are divided as shown below.
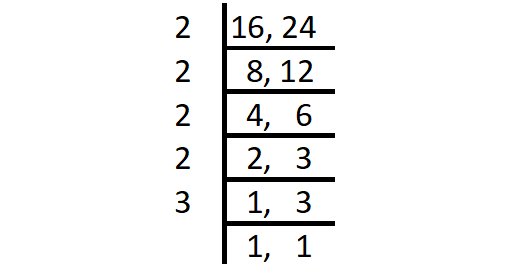
Step 2 :
LCM = Product of all prime factors
= 2 x 2 x 2 x 2 x 3
= 48
Thus, the LCM of 16 and 24 is 48.
Problem 4 :
Find the LCM of the following set of numbers using division method.
64, 80
Solution :
Step 1 :
Start with the smallest prime factor and go on dividing till all the numbers are divided as shown below.
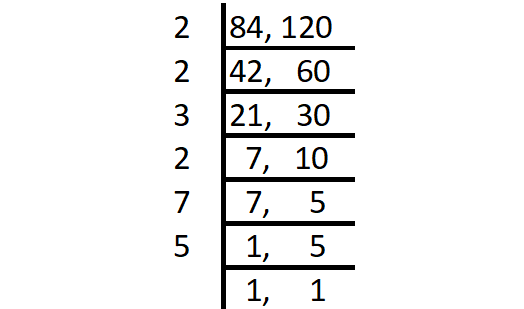
Step 2 :
LCM = Product of all prime factors
= 2 x 2 x 3 x 2 x 7 x 5
= 840
Thus, the LCM of 64 and 80 is 840.
Problem 5 :
Find the LCM of the following set of numbers using prime factorization method.
27, 45, 81
Solution :
Write the prime factors of 27, 45 and 81 as shown below.
27 = 3 x 3 x 3
45 = 3 x 3 x 5
81 = 3 x 3 x 3 x 3 x 3
The prime factor 3 appears a maximum of 5 times in the prime factorization of 81.
The prime factor 5 appears only 1 time in the prime factorization of 45.
Hence, the required LCM is
= (3 x 3 x 3 x 3 x 3) x 5
= 81 x 5
= 405
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4) -
10 Hard SAT Math Questions (Part - 3)
Jan 05, 26 06:34 PM
10 Hard SAT Math Questions (Part - 3)

