LEAST COMMON MULTIPLE BY PRIME FACTORIZATION

Least common multiple is the smallest number which is a multiple of the given numbers.

For example, consider the numbers 4 and 5.

The whole numbers which are multiples of both both 4 and 5 are

20, 40, 60, 80, ..........

All the above numbers are multiples of both 4 and 5.

Can we get a whole number less than 20 which is a multiple of both 4 and 5?

NO, we CAN'T.

So, 20 is the smallest whole number which is a multiple of both 4 and 5.

In other words, 20 is the smallest whole number which is evenly divisible by both 4 and 5.

Therefore, 20 is the least common multiple of 4 and 5.

More Examples :

Least common multiple of 2 and 3 = 6

Least common multiple of 4 and 6 = 12

Least common multiple of 3 and 6 = 6

In each case, find the least common multiple of the numbers by prime factorization.

Example 1 :

4 and 6

Solution :

Resolve the given numbers into their prime factors.

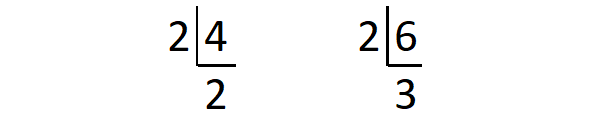
From the above division,

4 = 2 x 2

6 = 2 x 3

The different prime factors are 2 and 3.

The prime factor 2 appears a maximum of 2 times in the prime factorization of 4. 

The prime factor 3 appears a maximum of 1 time in the prime factorization of 6. 

Therefore, the least common multiple of 4 and 6 is

= 2 x 2 x 3

= 12

Example 2 :

2 and 3

Solution :

There is no common divisor for 2 and 3 other than 1. So, 2 and 3 are relatively prime.

To get least common multiple of relatively prime numbers, we have to multiply them.

Therefore, the least common multiple of 2 and 3 is

= 2 x 3

= 6

Example 3 :

4 and 5

Solution :

There is no common divisor for 4 and 5 other than 1. So, 4 and 5 are relatively prime.

To get least common multiple of relatively prime numbers, we have to multiply them.

Therefore, the least common multiple of 4 and 5 is

= 4 x 5

= 20

Example 4 :

3 and 6

Solution :

Since 3 is a prime number, we don't have to resolve it into prime factors anymore.

Resolve 6 into its prime factors.

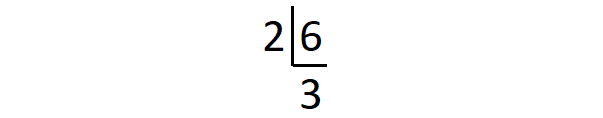
From the above division,

6 = 2 x 3

3 is already a prime number.

3 = 3

The different prime factors are 2 and 3.

The prime factor 2 appears a maximum of 1 time in the prime factorization of 6. 

The prime factor 3 appears a maximum of 1 time in the prime factorization of 6 and 3. 

Therefore, the least common multiple of 3 and 6 is

= 2 x 3

= 6

Example 5 :

12 and 18

Solution :

Resolve 12 and 18 into their prime factors.

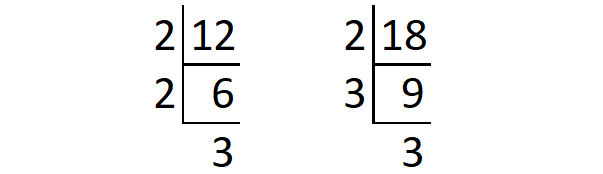
From the above division,

12 = 2 x 2 x 3

18 = 2 x 3 x 3

The different prime factors are 2 and 3.

The prime factor 2 appears a maximum of 2 times in the prime factorization of 12. 

The prime factor 3 appears a maximum of 2 times in the prime factorization of 18. 

Therefore, the least common multiple of 12 and 18 is

= 2 x 2 x 3 x 3

= 36

Example 6 :

24 and 60

Solution :

Resolve 24 and 60 into their prime factors.

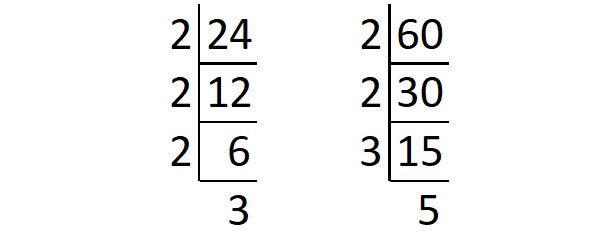
From the above division,

24 = 2 x 2 x 2 x 3

60 = 2 x 2 x 3 x 5

The different prime factors are 2, 3 and 5.

The prime factor 2 appears a maximum of 3 times in the prime factorization of 24. 

The prime factor 3 appears a maximum of 1 time in the prime factorization of 24 and 60.

The prime factor 5 appears a maximum of 1 time in the prime factorization of 60. 

Therefore, the least common multiple of 24 and 60 is

= 2 x 2 x 2 x 3 x 5

= 120

Example 7 :

4, 5 and 8

Solution :

Since 5 is a prime number, we don't have to resolve it into prime factors anymore.

Resolve 4 and 8 into their prime factors.

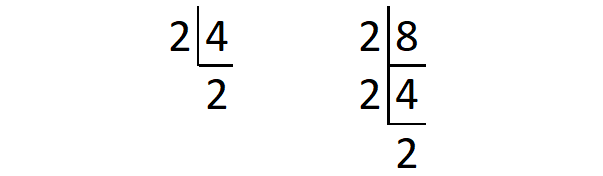
From the above division,

4 = 2 x 2

8 = 2 x 2 x 2

5 is already a prime number.

5 = 5

The different prime factors are 2 and 5.

The prime factor 2 appears a maximum of 3 times in the prime factorization of 8. 

The prime factor 5 appears a maximum of 1 time in the prime factorization of 5. 

Therefore, the least common multiple of 4, 5 and 8 is

= 2 x 2 x 2 x 5

= 40

Example 8 :

48, 72 and 108

Solution :

Resolve 48, 72 and 108 into their prime factors.

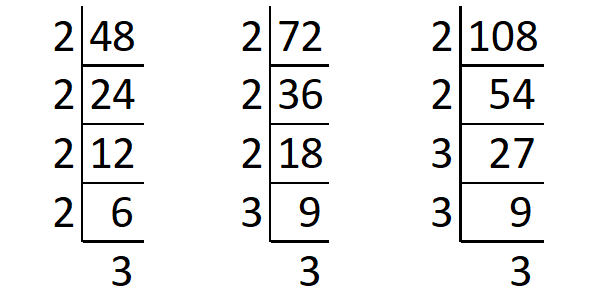
From the above division,

48 = 2 x 2 x 2 x 2 x 3

72 = 2 x 2 x 2 x 3 x 3

108 = 2 x 2 x 3 x 3 x 3

The different prime factors are 2 and 3.

The prime factor 2 appears a maximum of 4 times in the prime factorization of 48. 

The prime factor 3 appears a maximum of 3 times in the prime factorization of 108. 

Therefore, the least common multiple of 48, 72 and 108

= 2 x 2 x 2 x 2 x 3 x 3 x 3

= 432

Example 9 :

4, 6, 8 and 12

Solution :

Resolve 4, 6, 8 and 12 into their prime factors.

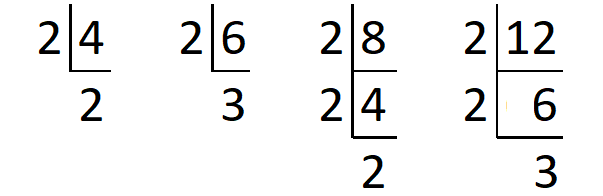
From the above division,

4 = 2 x 2

6 = 2 x 3

8 = 2 x 2 x 2

12 = 2 x 2 x 3

The different prime factors are 2 and 3.

The prime factor 2 appears a maximum of 3 times in the prime factorization of 8. 

The prime factor 3 appears a maximum of 1 time in the prime factorization of 6 and 12. 

Therefore, the least common multiple of 4, 6, 8 and 12 is

= 2 x 2 x 2 x 3

= 24

Example 10 :

2, 3, 4 and 5

Solution :

There is no common divisor for all the four numbers 2, 3, 4 and 5. So, the given numbers are relatively prime.

To get least common multiple of relatively prime numbers, we have to multiply them.

Therefore, the least common multiple of 2, 3, 4 and 5 is

= 2 x 3 x 4 x 5

= 120

Example 11 :

2, 4, 5 and 8

Solution :

Since 2 and 5 are prime numbers, we don't have to resolve them into prime factors anymore.

Resolve 4 and 8 into their prime factors.

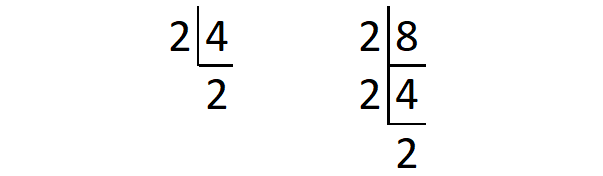
From the above division,

4 = 2 x 2

8 = 2 x 2 x 2

2 and 5 are already prime numbers.

2 = 2

5 = 5

The different prime factors are 2 and 5.

The prime factor 2 appears a maximum of 3 times in the prime factorization of 8. 

The prime factor 5 appears a maximum of 1 time in the prime factorization of 5. 

Therefore, the least common multiple of 2, 4, 5 and 8 is

= 2 x 2 x 2 x 5

= 40

Example 12 :

3, 6, 7 and 14

Solution :

Since 3 and 7 are prime numbers, we don't have to resolve them into prime factors anymore.

Resolve 6 and 14 into their prime factors.

From the above division,

6 = 2 x 3

14 = 2 x 7

3 and 7 are already prime numbers.

3 = 3

7 = 7

The different prime factors are 2, 3 and 7.

The prime factor 2 appears a maximum of 1 time in the prime factorization of 6 and 14.

The prime factor 3 appears a maximum of 1 time in the prime factorization of 6 and 3.

The prime factor 7 appears a maximum of 1 time in the prime factorization of 14 and 7. 

Therefore, the least common multiple of 3, 6, 7 and 14 is

= 2 x 3 x 7

= 42

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.