LAWS OF SINES AND COSINES PRACTICAL PROBLEMS

Problem 1 :

A plane is 1 km from one landmark and 2 km from another. From the planes point of view the land between them subtends an angle of 45°. How far apart are the landmarks?

Solution :

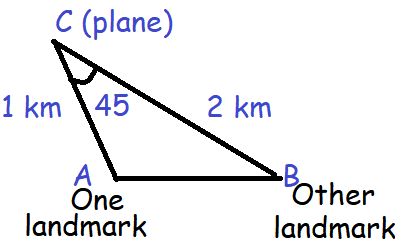
We have to find the length of AB.

a = 2 km (Opposite to angle A)

b = 1 km (Opposite to angle B)

c = AB (Opposite to angle C)

Cosine formula :

cos C  =  (a² + b² - c²) / 2ab

cos 45  =  (2² + 1² - c²) / 2(2)(1)

1/√2  =  (5 - c²) / 4

5 - c²  =  4/√2

5 - c²  =  2√2

c²  =  2√2 + 5

c  =  √(2√2 + 5)

Problem 2 :

A man starts his morning walk at a point A reaches two points B and C and finally back to A such that ∠A = 60^◦ and ∠B = 45^◦, AC = 4 km in the triangle ABC. Find the total distance he covered during his morning walk.

Solution :

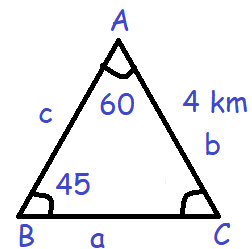
<A + <B + <C  =  180

60 + 45 + <C  =  180

<C  =  180 - 105  =  75

a/sin A  =  b/sin B  =  c/sin C

a/sin 60  =  4/sin 45  =  c/sin 75  ----(1)

First let us find "a".

a/sin 60  =  4/sin 45

a/(√3/2) =  4/(1/√2)

2a/√3  =  4√2

a  =  4√2√3/2

a  =  2√6

By applying a  =  2√6 in (1) and find c.

2√6/sin 60  =  c/sin 75 

2√6/(√3/2)  =  c/sin 75 

sin 75  =  sin (45 + 30)

  =  sin 45 cos 30 + cos 45 sin 30

  =  (1/√2) (√3/2) + (1/√2)(1/2)

  =  (√3 + 1)/2√2

4√2  =  c/(√3 + 1)/2√2

4√2  =  2√2c/(√3 + 1)

c  =  4√2(√3 + 1)/ 2√2

c  =  2(√3 + 1)

Total distance covered  =  2√6 + 4 + 2(√3 + 1)

 =  2√6 + 4 + 2√3 + 2

 =  2√6 + 6 + 2√3

Problem 3 :

Two vehicles leave the same place P at the same time moving along two different roads. One vehicle moves at an average speed of 60 km/hr and the other vehicle moves at an average speed of 80 km/hr. After half an hour the vehicle reach the destinations A and B. If AB subtends 60^◦ at the initial point P, then find AB. 

Solution :

Distance covered by A  =  time x speed 

  =  (1/2) ⋅ 60 

  =  30 km

Distance covered by B  =  time x speed 

  =  (1/2) ⋅ 80 

  =  40 km

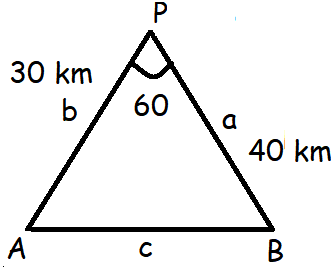
cos C  =  a² + b² - c²/2ab

cos 60 =  40² + 30² - c²/2(40)(30)

1/2  =  (1600 + 900 - c²)/2400

1200  =  2500 - c²

c²  =  2500 - 1200  =  1300

c = √1300

c  =  10√13

Hence the distance of A and B is  10√13 km.

Problem 4 :

Suppose that a satellite in space, an earth station and the center of earth all lie in the same plane. Let r be the radius of earth and R be the distance from the center of earth to the satellite. Let d be the distance from the earth station to the satellite. Let 30^◦ be the angle of elevation from the earth station to the satellite. If the line segment connecting earth station and satellite subtends angle α at the center of earth , then prove that d = R√1 + (r/R)² − 2 (r/R) cos α.

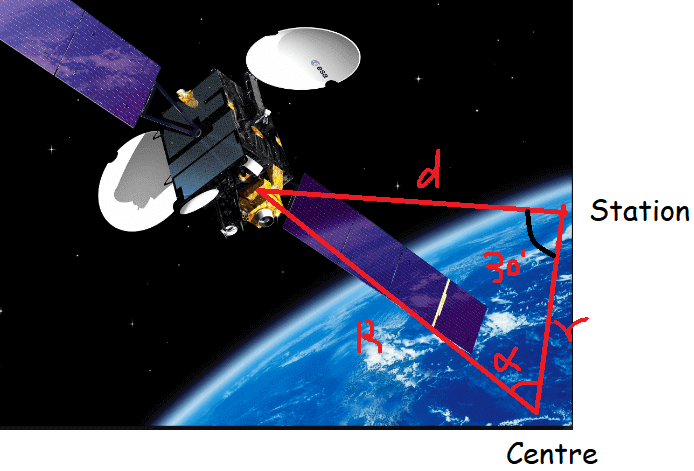
Solution :

Let A be the center, B be the station and C be the satellite position.

a/sin A  =  b/sin B  =  c/sin C

a = d, b = R and c = r

d/sin a  =  R/sin 30  = r/sin (180 - (30 +a))

cos A  =  (b² + c² - a²)/2bc

cos a  =  (R² + r² - d²)/2Rr

2Rr cos a  =  R² + r² - d²

d²  =  R² + r² - 2Rr cos a

d  =  √(R² + r² - 2Rr cos a)

d  =  √(R² (1 + (r/R)² - 2(r/R) cos a

d  =  R√(1 + (r/R)² - 2(r/R) cos a)

Hence proved.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.