LAWS OF COSINES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
The cosine law describes the relationship between the cosine of an angle and the lengths of the three sides of any triangle.
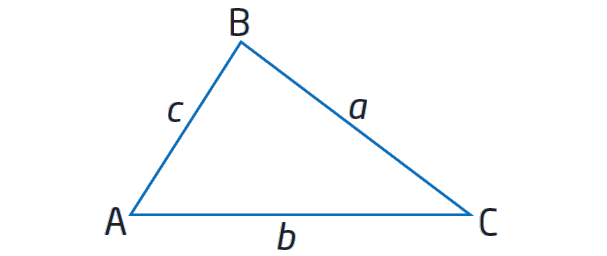
For any ΔABC, where a, b, and c are the lengths of the sides opposite to ∠A, ∠B, and ∠C, respectively, the cosine law states that
a2 = b2 + c2 - 2bc cos A
You can express the formula in different forms to find the lengths of the other sides of the triangle.
b2 = a2 + b2 - 2ab cos B
c2 = a2 + b2 - 2ab cos C
Proof :
In ΔABC, draw an altitude h.
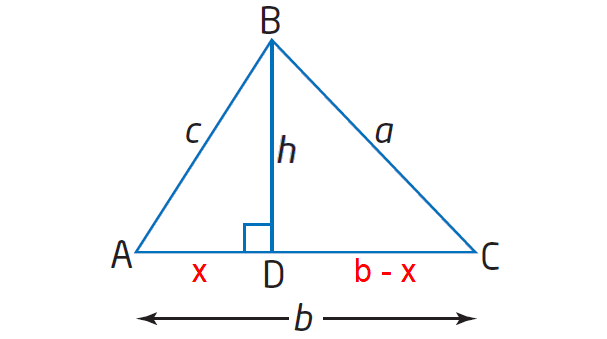
In ΔABD,
cos A = x/c
c cos A = x ----(1)
Using Pythagorean Theorem,
c2 = h2 + x2 ----(2)
In ΔBCD, using Pythagorean Theorem,
a2 = h2 + (b - x)2
a2 = h2 + (b - x)(b - x)
a2 = h2 + b2 - bx - bx + x2
a2 = h2 + b2 - 2bx + x2
a2 = h2 + x2 + b2 - 2bx
Substitute h2 + x2 = c2 [from (2)].
a2 = c2 + b2 - 2bx
a2 = b2 + c2 - 2bx
Substitute x = c cos A [from (1)].
a2 = b2 + c2 - 2b(c cos A)
a2 = b2 + c2 - 2bc cos A
Solved Problems
Problem 1 (Determining a Distance) :
A surveyor needs to find the length of a swampy area near Fishing Lake, Manitoba. The surveyor sets up her transit at a point A. She measures the distance to one end of the swamp as 468.2 m, the distance to the opposite end of the swamp as 692.6 m, and the angle of sight between the two as 78.6°. Determine the length of the swampy area, to the nearest tenth of a meter.
Solution :
Sketch a diagram to illustrate the problem.
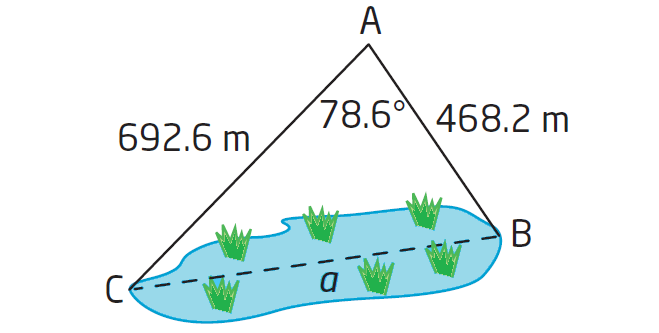
Using the cosine law,
a2 = b2 + c2 - 2bc cos A
Substitute b = 692.6, c = 468.2 and A = 78.6°.
a2 = 692.62 + 468.22 - 2(692.6)(468.2)cos 78.6°
a2 = 570715.205....
Taking square root on both sides,
a = √570715.205....
a = 755.456
The length of the swampy area is 755.5 m, to the nearest tenth of a meter.
Problem 2 (Determining an Angle) :
The Lions’ Gate Bridge has been a Vancouver landmark since it opened in 1938. It is the longest suspension bridge in Western Canada. The bridge is strengthened by triangular braces. Suppose one brace has side lengths 14 m, 19 m, and 12.2 m. Determine the measure of the angle opposite the 14-m side, to the nearest degree.
Solution :
Sketch a diagram to illustrate the problem.
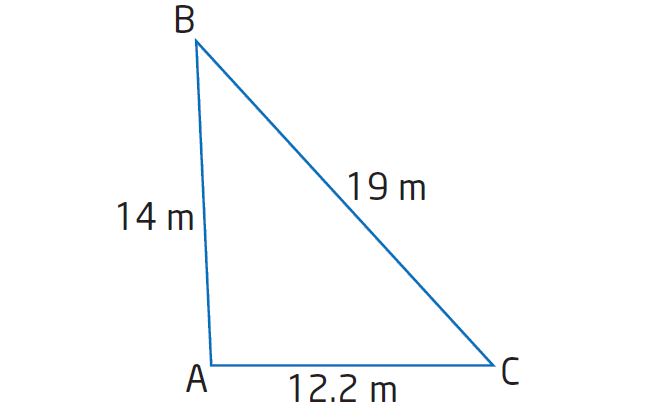
c2 = a2 + b2 - 2ab cos C
Substitute a = 19, b = 12.2 and c = 14.
142 = 192 + 12.22 - 2(19)(12.2) cos C
196 = 361 + 148.84 - 463.6 cos C
196 = 509.84 - 463.6 cos C
-313.84 = -463.6 cos C
Multiply both sides by -1.
313.84 = 463.6 cos C
Divide both sides by 463.6.
313.84/463.6 = cos C
cos-1(313.84/463.6) = ∠C
47.393.... = ∠C
The measure of the angle opposite the 14-m side is approximately 47°.
Problem 3 (Solve a Triangle) :
In ΔABC, a = 11, b = 5, and ∠C = 20°. Sketch a diagram and determine the length of the unknown side and the measures of the unknown angles, to the nearest tenth.
Solution :
Sketch a diagram of the triangle.
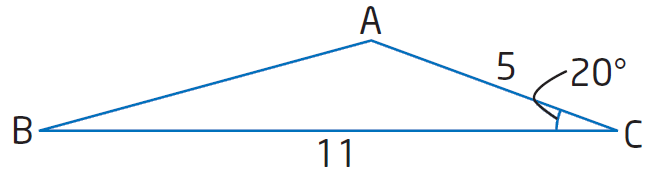
List the measures.
∠A = ? a = 11
∠B = ? b = 5
∠C = 20° c = ?
Use the cosine law to solve for c.
c2 = a2 + b2 - 2ab cos C
Substitute a = 11, b = 5 and C = 20°.
c2 = a2 + b2 - 2ab cos C
c2 = 112 + 52 - 2(11)(5) cos 20°
c2 = 121 + 25 - 110 cos 20°
c2 = 42.633....
Taking square root on both sides,
c = √42.633....
c = 6.529....
To solve for the angles, we can use the cosine law.
For ∠A :
a2 = b2 + c2 - 2bc cos A
Substitute a = 11, b = 5.... and c = 6.529.....
112 = 52 + (6.529....)2 - 2(5)(6.529) cos A
Solving the above equation for ∠A, we get
∠A = 15.2°
The six parts of the triangle are as follows:
|
∠A = 144.8° ∠B = 15.2° ∠C = 20° |
a = 11 b = 5 c = 6.5 |
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
90 Degree Clockwise Rotation
Jan 01, 26 06:58 AM
90 Degree Clockwise Rotation - Rule - Examples with step by step explanation -
US Common Core K-12 Curriculum Algebra Solving Systems of Equations
Jan 01, 26 04:51 AM
US Common Core K-12 Curriculum - Algebra : Solving Systems of Linear Equations -
Solving the HARDEST SAT Math Questions ONLY using Desmos
Dec 31, 25 05:53 AM
Solving the HARDEST SAT Math Questions ONLY using Desmos
