KEY FEATURES OF FUNCTIONS WORKSHEET

1. Find the domain and range of f(x).

f(x) = 3x + 4

2. Find the domain and range of g(x).

f(x) = √(2x - 4)

3. Find the x-intercepts.

y = x² - x - 6

4. Find the y-intercept.

y  =  2x - 3

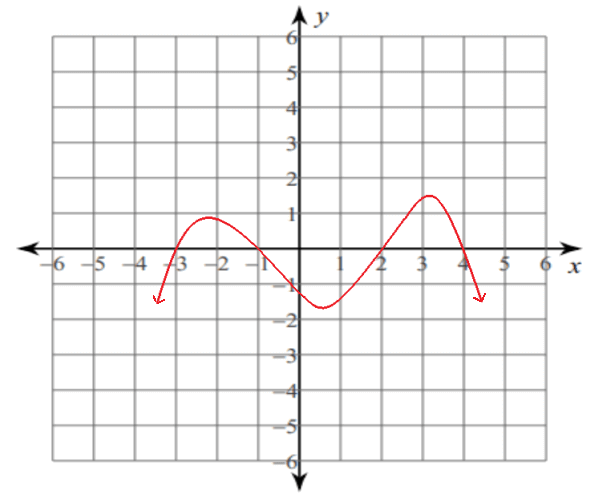
5. Find the positive and negative intervals of the function whose graph is shown below.

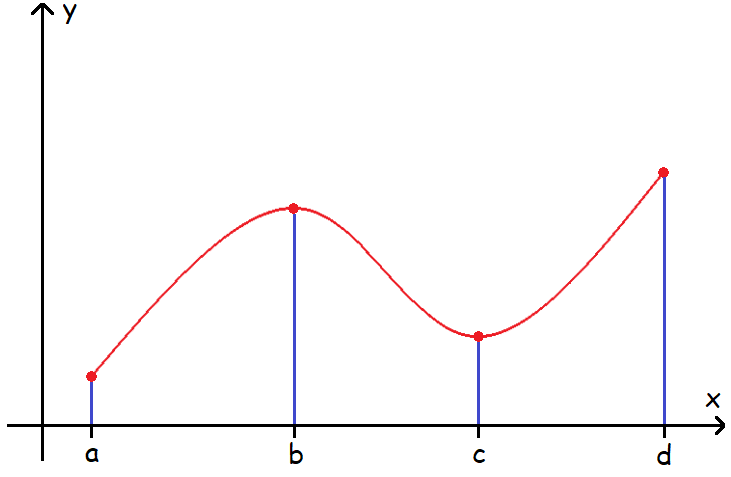
6. Find the intervals of increasing and decreasing of the function whose graph is shown below.

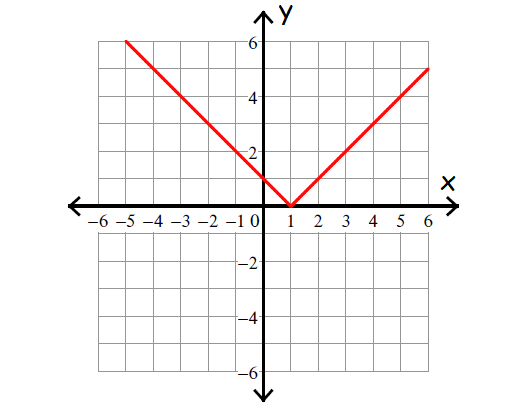
7. Find the parent function and baby function of the function whose graph is shown below.

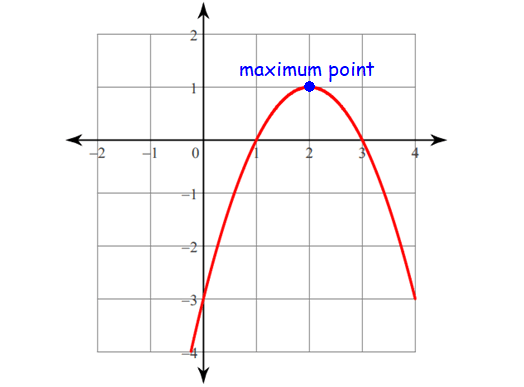
8. Find the parent function and baby function of the function whose graph is shown below.

9. Find the minimum point of the function :

f(x) = x² - 4x + 4

10. Find the minimum point of the function :

f(x) = -x² + 2x - 2

1. Answer :

f(x) = 3x + 4

Domain :

The given function is a linear function.

Here f(x) is defined for all real values of x.

So, the domain is all real values or x ∈ R.

Range :

Because the domain is all real values, we can substitute any real value for x in the given function f(x) = 3x + 4. When we substitute real values for x, we will be getting both positive and negative values for f(x).

Examples :

f(2) = 3(2) + 4 = 6 + 4 = 10

f(-3) = 3(-3) + 4 = -9 + 4 = -5

So, the range is also all real values or y ∈ R.

2. Answer :

f(x) = √(2x - 4)

Domain :

The given function is a radical function.

Here f(x) is defined, only if there is positive value inside the radical sign.

Then, we have

2x - 4 ≥ 0

Add 4 to each side.

2x ≥ 4

Divide each side by 2.

x ≥ 2

So, the domain is [2, ∞)

Range :

The given function is a radical function. In front of the radical sign, always we will have positive or negative sign. That is ±.

Example :

f(x) = ±√[2(3) - 4]

= ±√[6 - 4]

= ±√2

f(x) = √2 or f(x) = √2

When x ≥ 2, we get both positive and negative values for f(x).

So, the range is all real values" or y ∈ R.

3. Answer :

y = x² - x - 6

To find x-intercepts of a function, substitute 0 for y.

y = 0

x² - x - 6 = 0

Factor and solve.

(x + 2)(x - 3) = 0

x + 2 = 0 (or) x - 3 = 0

x = -2 or x = 3

So, the x-intercepts are -2 and 3.

4. Answer :

y = 2x - 3

To find y-intercept of a function, substitute 0 for x.

y = 2(0) - 3

y = -3

So, the y-intercept is  are -3.

5. Answer :

Positive Interval :

In the diagram above, the graph of the function is above the x-axis in the following intervals.

(-3, -1) and (2, 4)

More precisely, y is positive when x ∈ (-3, -1) and (2, 4).

So, the positive intervals for the above graph are

(-3, -1) and (2, 4)

Negative Interval :

In the diagram above, the graph of the function is below the x-axis in the following intervals.

(-∞, -3), (-1, 2) and (4, +∞)

More precisely, y is negative when x ∈ (-∞, -3), (-1, 2) and (4, +∞).

So, the negative intervals for the above graph are

(-∞, -3), (-1, 2) and (4, +∞)

6. Answer :

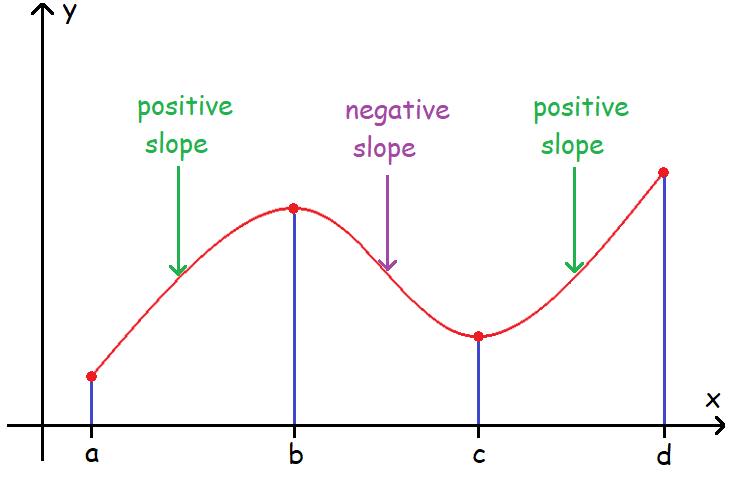
Interval of Increasing :

In the diagram above, clearly the graph is increasing in the intervals :

(a, b) and (c, d)

Interval of Decreasing :

In the diagram above, clearly the graph is decreasing in the interval :

(b, c)

7. Answer :

Parent Function :

The graph of the function shown above is in V shape.

So this is the graph of a absolute value function.

Hence, the parent function is

f(x) = |x|

Baby Function :

The baby function is the exact function of the graph shown above.

To find the Baby function, we can rewrite the parent function f(x) = |x| as shown below.

f(x) = |x - h| + k

Here, the vertex is (h, k).

Because the graph of the function shown above is in V shape and V is open upward, in front of the absolute value, we will have positive sign.

And also the vertex is (1, 0).

That is, (h, k) = (1, 0).

So, the Baby function of the graph shown above is

f(x) = |x - 1| + 0

f(x) = |x - 1|

8. Answer :

Parent Function :

The graph of the function shown above is a parabola.

So this is the graph of a quadratic function.

Hence, the parent function is

f(x) = x²

Baby Function :

The baby function is the exact function of the graph shown above.

To find the Baby function, we can rewrite the parent function f(x) = x² as shown below.

f(x) = (x - h)² + k

Here, the vertex is (h, k).

Because the graph of the function shown above is open downward parabola, the sign of (x - h)² will be negative.

Then, we have

f(x) = -(x - h)² + k

And also, the vertex is (2, 1).

That is, (h, k) = (2, 1).

So, the Baby function of the graph shown above is

f(x) = -(x - 2)² + 1

9. Answer :

f(x) = x² - 4x + 4

The given function is a quadratic function and its graph will be a parabola.

In the given function f(x) = x² - 4x + 4, since the sign of x² is positive, the parabola opens up and the minimum point is at the vertex.

Write the given quadratic function in vertex form.

f(x) = (x - h)² + k

Here, the vertex is (h, k).

f(x) = x² - 4x + 4

= x² - 2 ⋅ x ⋅ 2 + 2²

= (x - 2)²

f(x) = (x - 2)² + 0

The vertex of the parabola is (2, 0).

So, the minimum point is (2, 0).

10. Answer :

f(x) = -x² + 2x - 2

The given function is a quadratic function and its graph will be a parabola.

In the given function f(x) = -x² + 4x + 4, since the sign of x² is negative, the parabola opens down and the maximum point is at the vertex.

Write the given quadratic function in vertex form.

f(x) = -x² + 2x - 2

= -(x² - 2x) - 2

= -(x² - 2 ⋅ x ⋅ 1) - 2

= -(x² - 2 ⋅ x ⋅ 1 + 1² - 1²) - 2

= -[(x - 1)² - 1²] - 2

= -[(x - 1)² - 1] - 2

= -(x - 1)² + 1 - 2

f(x) = -(x - 1)² - 1

The vertex of the parabola is (1, -1).

So, the maximum point is (1, -1).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.