JUSTIFYING ANGLE RELATIONSHIPS WORKSHEET

Problem 1 :

A transversal cuts the two parallel lines and forms eight angles.  Describe the relationships between the angles in the diagram given below. 

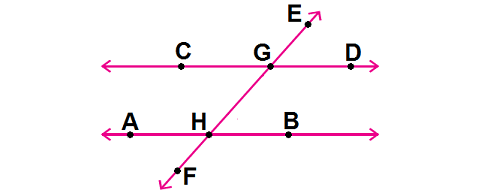
Problem 2 :

In the figure given below, let the lines l₁ and l₂ be parallel and m is transversal. If ∠F = 65°, using the angle relationships,  find the measure of each of the remaining angles.

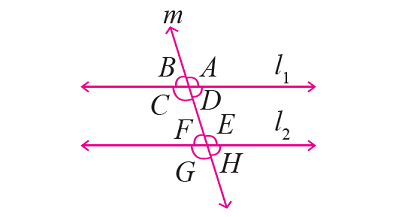
Problem 3 :

In the figure given below, let the lines l₁ and l₂ be parallel and t is transversal. Using angle relationships, find the value of x.

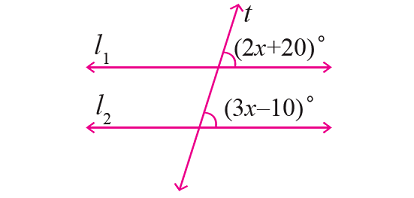
Problem 4 :

In the figure given below, let the lines l₁ and l₂ be parallel and t is transversal. Using angle relationships, find the value of x.

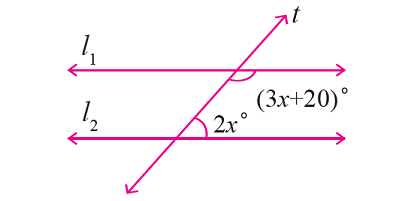
Answers

Problem 1 :

A transversal cuts the two parallel lines and forms eight angles.  Describe the relationships between the angles in the diagram given below. 

Answer :

Corresponding Angles : 

∠CGE and ∠AHG, ∠DGE and ∠BHG, ∠CGH and ∠AHF, ∠DGH and ∠BHF ; congruent.

Alternate Interior Angles :

∠CGH and ∠BHG, ∠DGH and ∠AHG ; congruent.

Alternate Exterior Angles :

∠CGE and ∠BHF, ∠DGE and ∠AHF ; congruent.

Same-Side Interior Angles :

∠CGH and ∠AHG, ∠DGH and ∠BHG ; supplementary.

Problem 2 : 

In the figure given below,  let the lines l₁ and l₂ be parallel and m is transversal. If ∠F = 65°, using the angle relationships,  find the measure of each of the remaining angles.

Answer :

From the given figure, 

∠F and ∠H are vertically opposite angles and they are equal. 

Then, ∠H  =  ∠F -------> ∠H  =  65°

∠H and ∠D are corresponding angles and they are equal. 

Then, ∠D  =  ∠H -------> ∠D  =  65°

∠D and ∠B are vertically opposite angles and they are equal. 

Then, ∠B  =  ∠D -------> ∠B  =  65°

∠F and ∠E are together form a straight angle.

Then, we have

∠F + ∠E  =  180°

Plug ∠F  =  65°

∠F + ∠E  =  180°

65° + ∠E  =  180°

∠E  =  115°

∠E and ∠G are vertically opposite angles and they are equal. 

Then, ∠G  =  ∠E -------> ∠G  =  115°

∠G and ∠C are corresponding angles and they are equal. 

Then, ∠C  =  ∠G -------> ∠C  =  115°

∠C and ∠A are vertically opposite angles and they are equal. 

Then, ∠A  =  ∠C -------> ∠A  =  115°

Therefore, 

∠A  =  ∠C  =  ∠E  =  ∠G  =  115°

∠B  =  ∠D  =  ∠F  =  ∠H  =  65°

Problem 3 :

In the figure given below,  let the lines l₁ and l₂ be parallel and t is transversal. Using angle relationships, find the value of x.

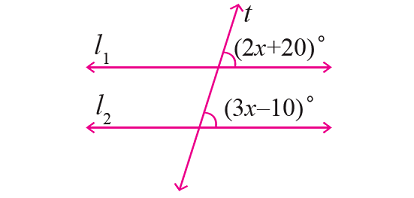
Answer :

From the given figure, 

∠(2x + 20)° and ∠(3x - 10)° are corresponding angles. 

So, they are equal. 

Then, we have

(2x + 20)°  =  (3x - 10)°

2x + 20  =  3x - 10

30  =  x

Problem 4 : 

In the figure given below,  let the lines l₁ and l₂ be parallel and t is transversal. Using angle relationships, find the value of x.

Answer :

From the given figure, 

∠(3x + 20)° and ∠2x° are consecutive interior angles. 

So, they are supplementary. 

Then, we have

(3x + 20)° + 2x°  =  180°

3x + 20 + 2x  =  180

5x + 20  =  180

5x  =  160

x  =  32

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.