ISOSCELES EQUILATERAL AND SCALENE TRIANGLE WORKSHEET

Problem 1 :

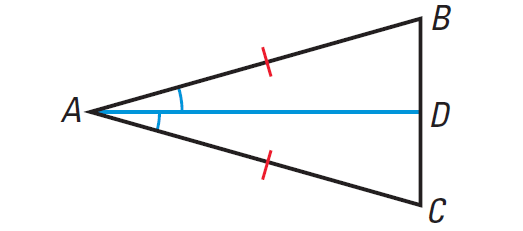
Use the diagram of ΔABC shown below to prove the Base Angles Theorem.

Problem 2 :

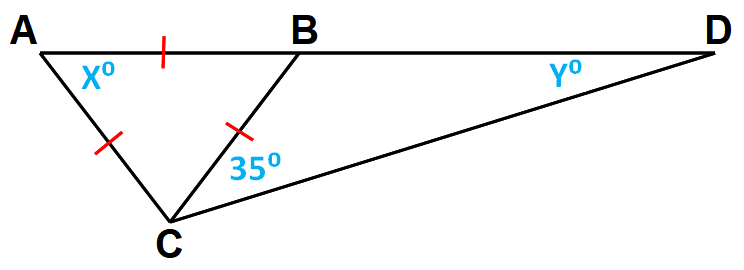
In the diagram shown below,

(i) find the value of x

(ii) find the value of y

Problem 3 :

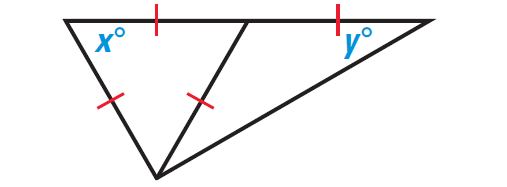
In the diagram shown below,

(i) find the value of x

(ii) find the value of y

Answers

1. Answer :

Given : In ΔABC, AB ≅ AC.

To prove : ∠B ≅ ∠C.

Proof :

(i) Draw the bisector of ∠CAB.

(ii) By construction, ∠CAD ≅ ∠BAD.

(iii) We are given that AB ≅ AC. Also DA ≅ DA, by the Reflexive Property of Congruence.

(iii) Use the SAS Congruence Postulate to conclude that ΔADB ≅ ΔADC.

(iv) Because corresponding parts of congruent triangles are congruent, it follows that ∠B ≅ ∠C.

2. Answer :

Part (i) :

In the diagram shown above, x represents the measure of an angle of an equilateral triangle.

From the corollary given above, if a triangle is equilateral, then it is equiangular.

So, the measure of each angle in the equilateral triangle is x.

By the Triangle Sum Theorem, we have

x° + x° + x° = 180°

Simplify. 

3x = 180

Divide both sides by 3 to solve for x.

x = 60

Part (ii) :

In the diagram shown above, the vertex angle forms a linear pair with a 60° angle, so its measure is 120°.

It has been illustrated in the diagram given below.

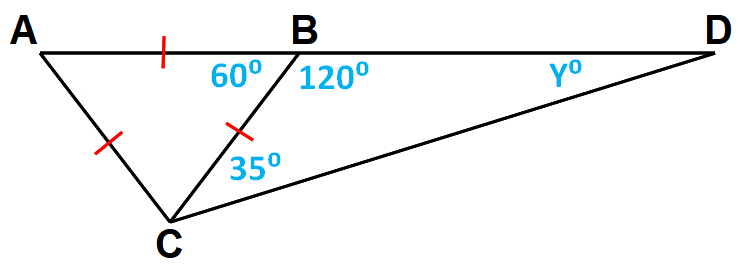
By the Triangle Sum Theorem, we have

120° + 35° + y° = 180°

Simplify.

155 + 2y = 180

Subtract 155 from both sides.

y = 25

3. Answer :

Part (i) :

In the diagram shown above, x represents the measure of an angle of an equilateral triangle.

From the corollary given above, if a triangle is equilateral, then it is equiangular.

So, the measure of each angle in the equilateral triangle is x.

By the Triangle Sum Theorem, we have

x° + x° + x° = 180°

Simplify. 

3x = 180

Divide both sides by 3 to solve for x.

x = 60

Part (ii) :

In the diagram shown above, y represents the measure of a base angle of an isosceles triangle.

From the Base Angles Theorem, the other base angle has the same measure. The vertex angle forms a linear pair with a 60° angle, so its measure is 120°.

It has been illustrated in the diagram given below.

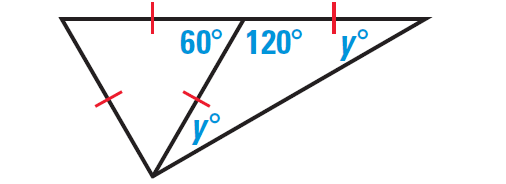
By the Triangle Sum Theorem, we have

120° + y° + y° = 180°

Simplify.

120° + 2y° = 180°

120 + 2y = 180

Subtract 120 from both sides.

2y = 60

Divide both sides by 2.

y = 30

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.