INVESTIGATING SYSTEMS OF EQUATIONS
We know the way to graph a linear equation in slope-intercept form. For example, we can use the slope and y-intercept or we can find two points that satisfy the equation and connect them with a line.
A. Graph the pair of equations together :
3x - y - 2 = 0
2x + y - 3 = 0
Let us re-write the given equations in slope-intercept form.
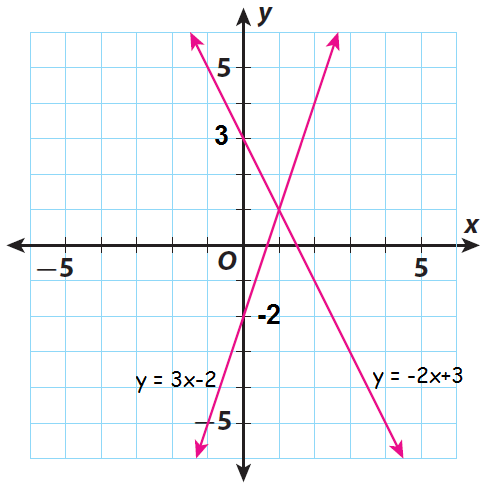
y = 3x - 2
(slope is 3 and y-intercept is -2)
y = -2x + 3
(slope is -2 and y-intercept is 3)
Based on slope and y-intercept, we can graph the given equations.
B. Explain how to say whether (3, -3) is a solution of the equation 3x - y - 2 = 0 without using the graph.
Substitute x = 3 and y = -3 in the equation 3x - y - 2 = 0.
3(3) - (-3) - 2 = 0 ?
9 - 3 - 2 = 0 ?
9 - 5 = 0 ?
4 = 0 ----> False
Substituting (3, -3) into the equation results in a false statement, so it is not a solution.
C. Explain how to say whether (3, -3) is a solution of the equation 2x + y - 3 = 0 without using the graph.
Substitute x = 3 and y = -3 in the equation 2x + y - 3 = 0.
2(3) + (-3) - 3 = 0 ?
6 - 3 - 3 = 0 ?
6 - 6 = 0 ?
0 = 0 ----> False
Substituting (3, -3) into the equation results in a true statement, so it is a solution.
D. Use the graph to explain whether (3, -3) is a solution of each equation.
If (3, -3) is on the line, it is a solution. If it is not on the line, it is not a solution.
(3, -3) is not on the line y = 3x - 2. So, (3, -3) is not a solution of y = 3x - 2 or 3x - y - 2 = 0.
But (3, -3) is on the line y = -2x + 3, so (3, -3) is a solution of y = -2x + 3 or 2x + y - 3 = 0.
E. Determine if the point of intersection is a solution of both equations.
Point of intersection : (1, 1).
Because (1, 1) satisfies both the equations.
3(1) - 1 - 2 = 0
3 - 1 - 2 = 0
3 - 3 = 0
0 = 0
2x + y - 3 = 0
2(1) + 1 - 3 = 0
2 + 1 - 3 = 0
0 = 0
So, the point of intersection is the solution of both equations.
Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.
You can also visit the following web pages on different stuff in math.
WORD PROBLEMS
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Trigonometry word problems
Markup and markdown word problems
Word problems on mixed fractrions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Word problems on sets and venn diagrams
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Time, speed and distance shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the word problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by 7
Sum of all three digit numbers divisible by 8
Sum of all three digit numbers formed using 1, 3, 4
Sum of all three four digit numbers formed with non zero digits
Recent Articles
-
Comparing Fractions
Aug 04, 20 12:29 PM
Comparing Fractions - Examples with step by step explanation
-
Comparing Fractions Worksheet
Aug 04, 20 12:26 PM
Comparing Fractions Worksheet
-
Comparing and Ordering Decimals Worksheet
Aug 04, 20 12:23 PM
Comparing and Ordering Decimals Worksheet
