INVESTIGATING SLOPE AND Y-INTERCEPT

The graph of every non vertical line crosses the y-axis. The y-intercept is the y-coordinate of the point where the graph intersects the y-axis. The x-coordinate of this point is always 0.

The graph given below represents the linear equation

y  =  (-2/3)x + 4

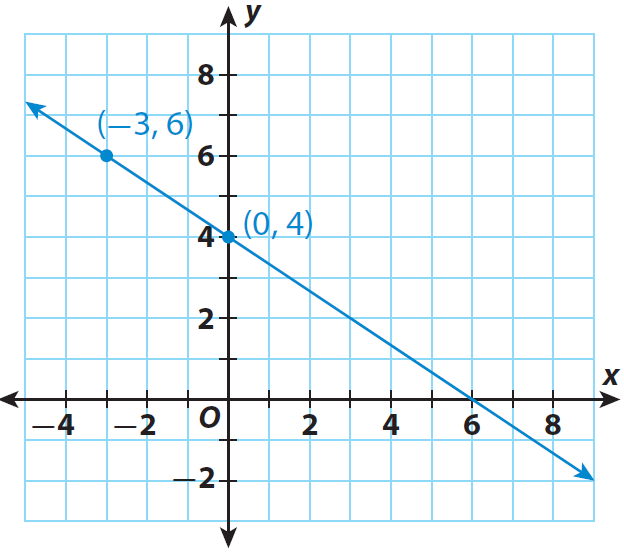
Step 1 :

Find the slope of the line using the points (0,4) and (-3,6).

m  =  change in y-values / change in x-values

m  =  (6 - 4) / (-3 - 0)

m  =  2/(-3)

m  =  -2/3

Step 2 :

The line also contains the point (6, 0). What is the slope using (0, 4) and (6, 0)? Using (-3, 6) and (6, 0). What do you notice ?

m  =  change in y-values / change in x-values

m  =  (0 - 4) / (6 - 0)

m  =  -4/6

m  =  -2/3

It is the same as in Step 1.

Step 3 :

Find the value of y when x = 0 using the equation y = (-2/3)x + 4. Describe the point on the graph that corresponds to this solution.

4 ; (0, 4) is where the line intersects the y-axis.

Step 4 :

Compare your answer in Step 4 with the equation of the line.

The number 4 is the same as the number that is added to the x-term in the equation y = (-2/3)x + 4.

Step 5 :

After having discussed the above four steps, can we find the slope and y-intercept from the equation y = (-2/3)x + 4 without any calculation ?

Yes

The coefficient of x is slope and the number added to x-term is y-intercept. 

That is, 

Slope  =  -2/3

y-intercept  =  4

Step 6 :

When can we find the slope and y-intercept of a line directly from the equation without any calculation ?

When the equation of a straight line is given in the form

y = mx + b,

we will be able to get slope and y-intercept of the line directly from the equation without any calculation. 

That is, 

slope  =  m

y-intercept  =  b

And also, the form y = mx + b is called slope intercept form equation of a straight line. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.